|
Mfocus1590
Figure 2 First frame of movie generated by wavemovie(). (Press button for movie.) | 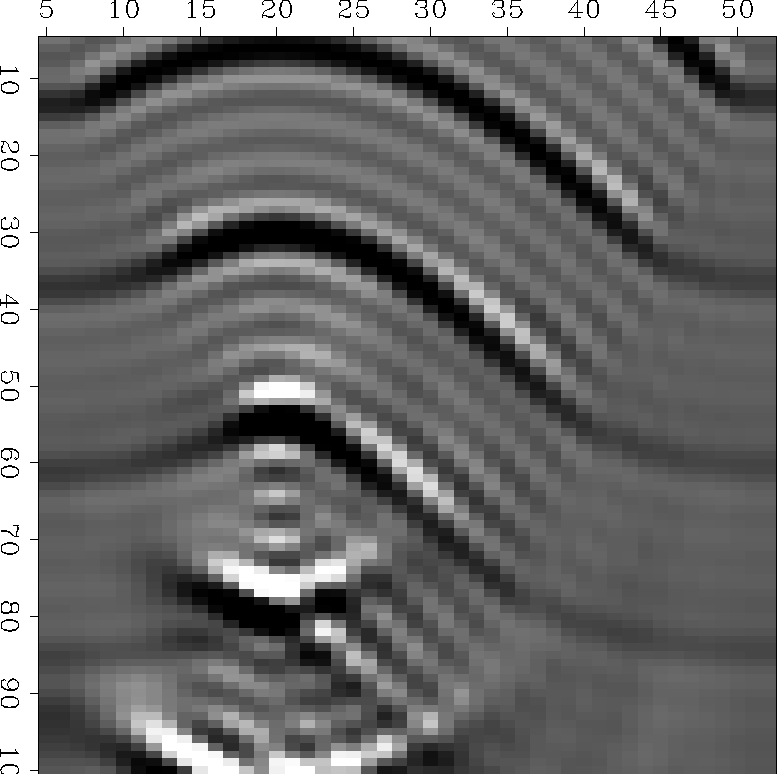 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Here we see solutions to exercises stated in figure captions. The problems and solutions were worked over by former teaching assistants. (Lynn, Gonzalez, JFC, Hale, Li, Karrenbach, Fomel). The various figures are all variations of the computer subroutine wavemovie(). It makes a movie of a sum of monochromatic waves. As it stands it will produce a movie (three-dimensional matrix) of waves propagating through a focus. The whole process from compilation through computation to finally viewing the film loop takes a few seconds. A sample frame of the movie is in Figure 2.
|
Mfocus1590
Figure 2 First frame of movie generated by wavemovie(). (Press button for movie.) |  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
It shows a snapshot of the (x,z)-plane.
Collapsing spherical waves enter from the top,
go through a focus and then expand again.
Notice that the wavefield is small but not zero in the region
of geometrical shadow.
In the shadow region you see waves that appear to be circles
emanating from point sources at the top corners.
Notice that the amplitudes of expanding spherical waves
drop off with distance and collapsing spherical waves grow
towards the focus.
We will study the program that made this figure
and see many features of waves
and mathematics.