




Next: Constant offset migration
Up: PRESTACK MIGRATION
Previous: Cheops' pyramid
Equation (1) in (y,h)-space is
| 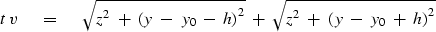 |
(5) |
A basic insight into equation (1) is to notice
that at constant-offset h and constant travel time t
the locus of possible reflectors is
an ellipse in the (y ,z)-plane centered at y0.
The reason it is an ellipse
follows from the geometric definition of an ellipse.
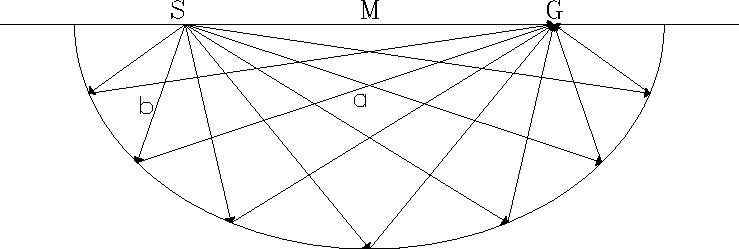
To draw an ellipse,
place a nail or tack into s on Figure 1
and another into g.
Connect the tacks by a string
that is exactly long enough to go through (y0 ,z).
An ellipse going through (y0 ,z) may be constructed
by sliding a pencil along the string,
keeping the string tight.
The string keeps the total distance tv constant as is shown in
Figure 3
ellipse1
Figure 3
Prestack migration ellipse, the locus of all scatterers with
constant traveltime for source S and receiver G.
|
|  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Replacing depth z in equation (5)
by the vertical traveltime depth
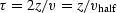 we get
we get
| ![\begin{displaymath}
t \eq {1 \over 2}\
\left(
\sqrt { \tau^2\ +\ [( y-y_0)-h]^...
...rt { \tau^2\ +\ [( y-y_0)+h]^2 / v_{\rm half}^2 }
\
\right)\end{displaymath}](img7.gif) |
(6) |





Next: Constant offset migration
Up: PRESTACK MIGRATION
Previous: Cheops' pyramid
Stanford Exploration Project
12/26/2000

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![]() we get
we get