




Next: DMO IN THE PROCESSING
Up: GARDNER'S SMEAR OPERATOR
Previous: GARDNER'S SMEAR OPERATOR
Recall equation (9)
for an ellipse centered at the origin.
| 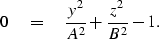 |
(19) |
where
|  |
(20) |
|  |
(21) |
The ray goes from the shot at one focus of the ellipse
to anywhere on the ellipse,
and then to the receiver in traveltime th.
The equation for a circle of radius 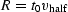 with center on the surface
at the source-receiver pair coordinate x=b is
with center on the surface
at the source-receiver pair coordinate x=b is
| 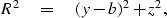 |
(22) |
where
|  |
(23) |
To get the circle and ellipse tangent to each other,
their slopes must match.
Implicit differentiation of equation (19) and (22)
with respect to y yields:
| 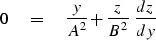 |
(24) |
| 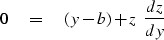 |
(25) |
Eliminating dz/dy from equations (24) and (25) yields:
| 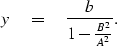 |
(26) |
At the point of tangency the circle and the ellipse should coincide.
Thus we need to combine equations to eliminate x and z.
We eliminate z from equation (19) and (22)
to get an equation only dependent on the y variable.
This y variable can be eliminated by inserting equation (26).
| 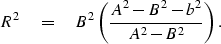 |
(27) |
Substituting the definitions (20), (21),
(23) of various parameter gives the
relation between zero-offset traveltime t0 and nonzero traveltime
th:
| 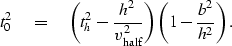 |
(28) |
As with the Rocca operator, equation (28)
includes both dip moveout DMO and NMO.





Next: DMO IN THE PROCESSING
Up: GARDNER'S SMEAR OPERATOR
Previous: GARDNER'S SMEAR OPERATOR
Stanford Exploration Project
12/26/2000
![]() with center on the surface
at the source-receiver pair coordinate x=b is
with center on the surface
at the source-receiver pair coordinate x=b is