Migration and diffraction operators can be conceived
and programmed in two different ways.
Let ![]() denote data and
denote data and ![]() denote the depth image.
We have
denote the depth image.
We have
| (14) | ||
| (15) |
| (16) | ||
| (17) |
Given a nonzero-offset section,
we seek to convert it to a zero-offset section.
Rocca's concept is to first migrate the constant offset data
with an ellipsoid push operator ![]() and then take each point on the ellipsoid
and diffract it out to a zero-offset hyperbola
with a push operator
and then take each point on the ellipsoid
and diffract it out to a zero-offset hyperbola
with a push operator ![]() .The product of push operators
.The product of push operators
![]() is known as Rocca's smile.
This smile operator includes both normal moveout and dip moveout.
(We could say that dip moveout is defined by Rocca's smile
after restoring the normal moveout.)
is known as Rocca's smile.
This smile operator includes both normal moveout and dip moveout.
(We could say that dip moveout is defined by Rocca's smile
after restoring the normal moveout.)
Because of the approximation ![]() ,we have four different ways to express the Rocca smile:
,we have four different ways to express the Rocca smile:
| |
(18) |
The operator ![]() ,having two pull operators should have smoothest output.
Sergey Fomel suggests an interesting illustration of it:
Its adjoint is two push operators,
,having two pull operators should have smoothest output.
Sergey Fomel suggests an interesting illustration of it:
Its adjoint is two push operators,
![]() .
.![]() takes us from zero offset to nonzero offset
first by pushing a data point to a semicircle
and then by pushing points on the semicircle to flat-topped hyperbolas.
As before, to make the hyperbolas more distinct,
I broke the circle into dots along the circle
and show the result in Figure 20.
The whole truth is a little more complicated.
Subroutine flathyp()
takes us from zero offset to nonzero offset
first by pushing a data point to a semicircle
and then by pushing points on the semicircle to flat-topped hyperbolas.
As before, to make the hyperbolas more distinct,
I broke the circle into dots along the circle
and show the result in Figure 20.
The whole truth is a little more complicated.
Subroutine flathyp() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) implements
implements ![]() and
and ![]() .Since I had no subroutine for
.Since I had no subroutine for ![]() ,figures 18 and 20
were actually made with only
,figures 18 and 20
were actually made with only ![]() and
and ![]() .
.
|
sergey
Figure 20 The adjoint of Rocca's smile is a superposition of flattened hyperbolas, each with its top on a circle. | 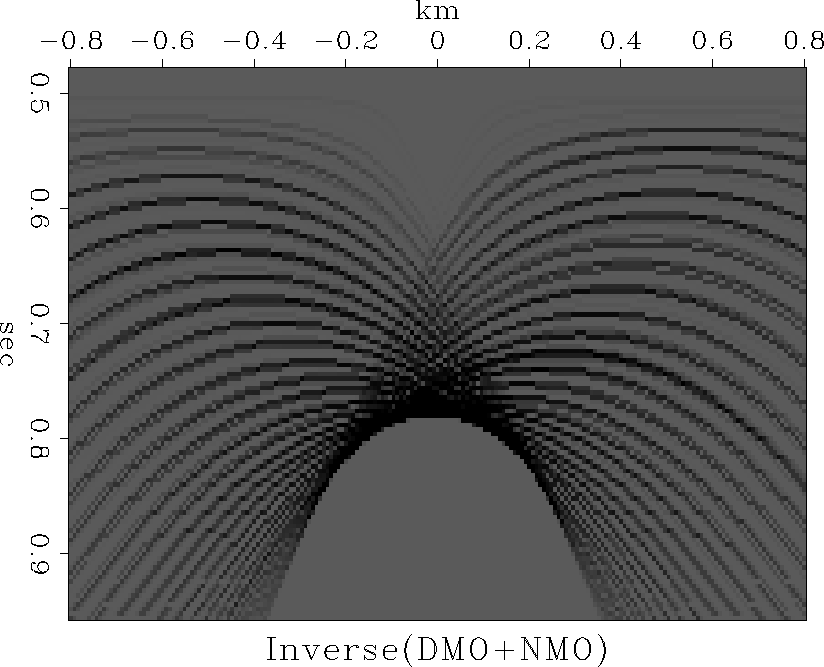 |
We discuss the
![]() representation of
representation of ![]() in the next section.
in the next section.