




Next: Nearest-neighbor coordinates
Up: FAMILIAR OPERATORS
Previous: Zero padding is the
Here we examine an example of the general idea that
adjoints of products are reverse-ordered products of adjoints.
For this example we use the Fourier transformation.
No details of Fourier transformation are given here
and we merely use it as an example of a square matrix 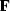 .We denote the complex-conjugate transpose (or adjoint) matrix
with a prime,
i.e.,
.We denote the complex-conjugate transpose (or adjoint) matrix
with a prime,
i.e., 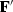 .The adjoint arises naturally whenever we consider energy.
The statement that Fourier transforms conserve energy is
.The adjoint arises naturally whenever we consider energy.
The statement that Fourier transforms conserve energy is
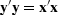 where
where 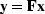 .Substituting gives
.Substituting gives 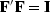 , which shows that
the inverse matrix to Fourier transform
happens to be the complex conjugate of the transpose of
, which shows that
the inverse matrix to Fourier transform
happens to be the complex conjugate of the transpose of  .
.
With Fourier transforms,
zero padding and truncation are especially prevalent.
Most subroutines transform a dataset of length of 2n,
whereas dataset lengths are often of length 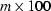 .The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation
.The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation  can be expressed in matrix algebra as
can be expressed in matrix algebra as
| ![\begin{displaymath}
{\rm Program} \eq
\bold F \
\left[
\begin{array}
{c}
\bold I \\
\bold 0
\end{array} \right] \end{displaymath}](img28.gif) |
(6) |
According to matrix algebra, the transpose of a product,
say 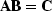 ,is the product
,is the product 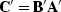 in reverse order.
So the adjoint subroutine is given by
in reverse order.
So the adjoint subroutine is given by
| ![\begin{displaymath}
{\rm Program'} \eq
\left[
\begin{array}
{cc}
\bold I & \bold 0
\end{array} \right]
\
\bold F'\end{displaymath}](img31.gif) |
(7) |
Thus the adjoint subroutine
truncates the data after the inverse Fourier transform.
This concrete example illustrates that common sense often represents
the mathematical abstraction
that adjoints of products are reverse-ordered products of adjoints.
It is also nice to see a formal mathematical notation
for a practical necessity.
Making an approximation need not lead to collapse of all precise analysis.





Next: Nearest-neighbor coordinates
Up: FAMILIAR OPERATORS
Previous: Zero padding is the
Stanford Exploration Project
12/26/2000
![]() .The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation
.The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation ![]() can be expressed in matrix algebra as
can be expressed in matrix algebra as