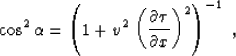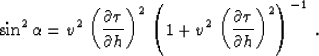Next: Conclusions
Up: FROM KINEMATICS TO DYNAMICS
Previous: Dynamics of Residual NMO
The case of residual DMO complicates building of a dynamic equation
because of the essential nonlinearity of the kinematic equation
(32). One possible way to linearize the problem is to increase
the order of the equation. In this case, the resultant dynamic
equation would include a term with the second-order derivative with
respect to velocity v. Such an equation describes two different
modes of wave propagation and requires additional initial conditions
to separate them. Another possible way to linearize equation
(32) is to approximate it at small dip angles. For example, one
can obtain a recursively accurate approximation by a continuous
fraction expansion of the square root in equation (32),
analogously to Muir's method in conventional finite-difference
migration Claerbout (1985). In this case, the dynamic
equation would contain only the first-order derivative with respect to
the velocity and high-order derivatives with respect to other
parameters. The third, and probably the most attractive, method is to
change the domain of consideration. For example, we could switch from
the common-offset domain to the domain of common offset dip. This
method implies a transformation similar to slant stacking of
common-midpoint gathers in the post-migration domain in order to
obtain the local offset dip information. Equation (32)
transforms, with the help of the results from Appendix A, to the form
| 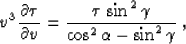 |
(60) |
with
| 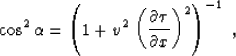 |
(61) |
and
| 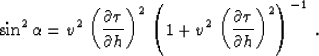 |
(62) |
For a constant offset dip 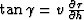 , the dynamic analogue of equation (60) is the
third-order partial differential equation
, the dynamic analogue of equation (60) is the
third-order partial differential equation
| 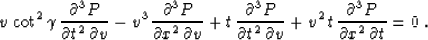 |
(63) |
Equation (63) doesn't strictly comply with the theory of
second-order linear differential equations. Its properties and
practical applicability require further research.





Next: Conclusions
Up: FROM KINEMATICS TO DYNAMICS
Previous: Dynamics of Residual NMO
Stanford Exploration Project
9/12/2000