




Next: Dynamics of Residual NMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: FROM KINEMATICS TO DYNAMICS
In the case of zero-offset velocity continuation, the characteristic
equation is reconstructed from equation (2) to have the form
| 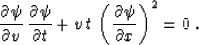 |
(50) |
According to formula (46), the corresponding dynamic equation is
| 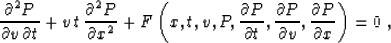 |
(51) |
where the function F remains to be defined. The simplest case of F
equal to zero corresponds to Claerbout's velocity continuation
equation Claerbout (1986), derived in a different way. Levin
1986a provides the dispersion-relation
derivation, conceptually analogous to applying the method of
characteristics.
In high-frequency asymptotics, the wavefield P can be
represented by the ray-theoretical (WKBJ) approximation,
| 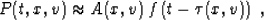 |
(52) |
where A is the amplitude, f is the short (high-frequency) wavelet,
and the function  satisfies the kinematic equation
(2). Substituting approximation (52) into the dynamic
velocity continuation equation (51), collecting the
leading-order terms, and neglecting the F function, we arrive at the
partial differential equation for amplitude transport:
satisfies the kinematic equation
(2). Substituting approximation (52) into the dynamic
velocity continuation equation (51), collecting the
leading-order terms, and neglecting the F function, we arrive at the
partial differential equation for amplitude transport:
| 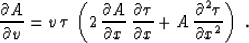 |
(53) |
The general solution of equation (53) follows from the
theory of characteristics. It takes the form
| 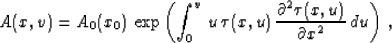 |
(54) |
where A0(x0) = A(x,0), and the integral corresponds to the
curvilinear integration along the corresponding velocity ray.
In the case of a plane dipping reflector, the image of the reflector remains
plane in the velocity continuation process. Therefore, the second
traveltime derivative 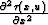 in
(54) equals zero, and the exponential is equal to
one. This means that the amplitude of the image doesn't change with
the velocity along the velocity rays. This fact doesn't agree with the
theory of conventional post-stack migration, which suggests
downscaling the image by the ``cosine'' factor
in
(54) equals zero, and the exponential is equal to
one. This means that the amplitude of the image doesn't change with
the velocity along the velocity rays. This fact doesn't agree with the
theory of conventional post-stack migration, which suggests
downscaling the image by the ``cosine'' factor 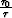 Chun and Jacewitz (1981); Levin (1986b). The simplest way to
include the cosine factor in the velocity continuation equation is to
set the function F to be
Chun and Jacewitz (1981); Levin (1986b). The simplest way to
include the cosine factor in the velocity continuation equation is to
set the function F to be 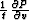 . The resulting differential equation
. The resulting differential equation
| 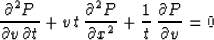 |
(55) |
has the amplitude transport
| 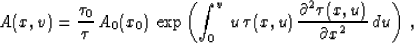 |
(56) |
corresponding to the differential equation
| 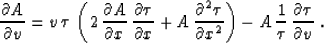 |
(57) |
Appendix B proves that the time-and-space solution of the dynamic
velocity continuation equation (55) coincides with the
conventional Kirchhoff migration operator.
The finite-difference implementation of zero-offset velocity
continuation resembles the implementation of Claerbout's
15-degree equation in a retarded coordinate system
Claerbout (1976). This implementation is discussed in
more detail in Appendix C.





Next: Dynamics of Residual NMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: FROM KINEMATICS TO DYNAMICS
Stanford Exploration Project
9/12/2000