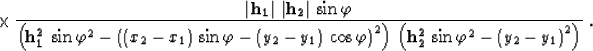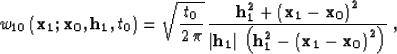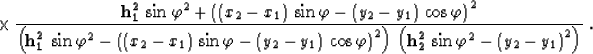AMO AMPLITUDE

The weighting function of the AMO operator can be determined from cascading the DMO and inverse DMO operators by means of equation (10). In the case of Hale's DMO Hale (1984) and its adjoint Ronen (1987),  

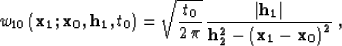$$w_{10}\left({\bf x_1;x_0, h_1},t_0\right) = \sqrt{t_0 \over... ...\vert h_1\right\vert} \over {h_2^2-\left(x_1-x_0\right)^2}}}\;,$$ (22)

 

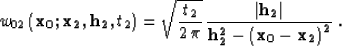$$w_{02}\left({\bf x_0;x_2, h_2},t_2\right) = \sqrt{t_2 \over... ...\vert h_2\right\vert} \over {h_2^2-\left(x_0-x_2\right)^2}}}\;.$$ (23)

As follows from (A-1),(A-2), and (10),

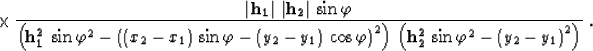$$\begin{eqnarray} \times\, {{{\bf \left\vert h_1\right\vert\,\left\vert h_2\right... ...ft({\bf h_2^2}\,\sin{\varphi}^2-\left(y_2-y_1\right)^2\right)}}\;.\end{eqnarray}$$ (24)

In the case of the so-called true-amplitude DMO Black et al. (1993) and its asymptotic inverse,  

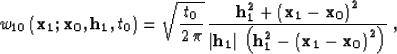$$w_{10}\left({\bf x_1;x_0, h_1},t_0\right) = \sqrt{t_0 \over... ...t h_1\right\vert\,\left(h_1^2-\left(x_1-x_0\right)^2\right)}\;,$$ (25)

 

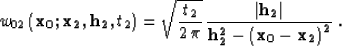$$w_{02}\left({\bf x_0;x_2, h_2},t_2\right) = \sqrt{t_2 \over... ...\vert h_2\right\vert} \over {h_2^2-\left(x_0-x_2\right)^2}}}\;.$$ (26)

Inserting (A-4) and (A-5) into (10) yields

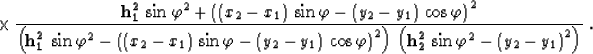$$\begin{eqnarray} \times\, {{{\bf h_1^2}\,\sin{\varphi}^2+ \left(\left(x_2-x_1\ri... ...ft({\bf h_2^2}\,\sin{\varphi}^2-\left(y_2-y_1\right)^2\right)}}\;.\end{eqnarray}$$ (27)