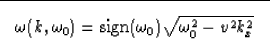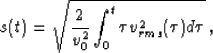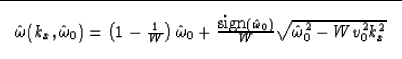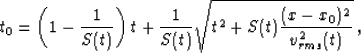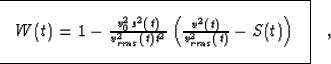Next: Application
Up: Vaillant & Fomel: On
Previous: Introduction
Stolt time migration can be summarized as the following sequence of
transformations:
| 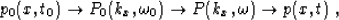 |
(1) |
where
| 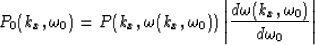 |
(2) |
The function 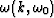 is the dispersion relation and has
the following expression in the constant velocity case:
is the dispersion relation and has
the following expression in the constant velocity case:
| 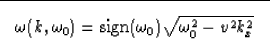 |
(3) |
The approximation suggested by Stolt 1978 for
extending the method to v(z) media involves a change of the time
variable (Stolt-stretch):
| 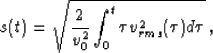 |
(4) |
where s(t) is the stretched time variable, v0 is an arbitrarily chosen constant velocity, and vrms(t)
is the root mean square velocity along the vertical ray,
defined by
| 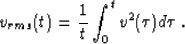 |
(5) |
This change of variable yields a transformed wave-equation for the
wavefield extrapolation, in which Stolt replaces a slowly
varying complicated function of several parameters (denoted by W)
by its average value. Making this
approximation yields a new dispersion relation in the transformed
coordinate system:
| 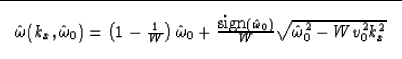 |
(6) |
This factor W contains all the information about the heterogeneities
of the medium. However, it has to be determined a priori, that is,
before migration.
This empirical choice for W was one of the drawbacks of the
Stolt-stretch method. Fomel 1995 derived an
analytical formulation of the Stolt-stretch parameter, based on
Malovichko's formula for approximating traveltimes in vertically
inhomogeneous media Malovichko (1978):
| 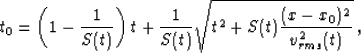 |
(7) |
where the function S(t) defines the so-called parameter of heterogeneity:
| 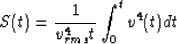 |
(8) |
Fomel proved that, for a given depth (or vertical traveltime), the
optimal value of W is
| 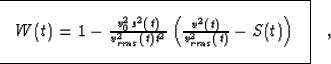 |
(9) |
where vrms(t) is the root mean square velocity along the
vertical ray, and 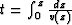 the vertical
traveltime. The value of W used during Stolt migration is the
average along the vertical profile of these W(t).
In the case of an homogeneous constant-velocity model, W is equal to
1.0, whereas it has to be less than 1.0 if the velocity increases
monotonically with depth.
the vertical
traveltime. The value of W used during Stolt migration is the
average along the vertical profile of these W(t).
In the case of an homogeneous constant-velocity model, W is equal to
1.0, whereas it has to be less than 1.0 if the velocity increases
monotonically with depth.
We can sum up the application of Stolt-stretch algorithm with the
optimal parameter W by the following sequence of steps:
| 1. Stretch the time axis and determine |
|---|
| the value of W along the vertical profile |
| 2. Interpolate stretched time to a regular grid |
|---|
| 3. 2-D FFT |
|---|
| 4. Apply Stolt migration with the dispersion relation (6) |
|---|
| 5. 2-D inverse FFT |
|---|
| 6. Unstretch the time axis |
|---|





Next: Application
Up: Vaillant & Fomel: On
Previous: Introduction
Stanford Exploration Project
5/1/2000