Next: Offset Continuation and DMO
Up: EXAMPLES
Previous: Post-Stack Residual Migration
Velocity transform is another form of hyperbolic stacking with the
summation path
| 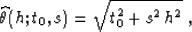 |
(81) |
where h corresponds to the offset, s is the stacking slowness, and
t0 is the estimated zero-offset traveltime. Hyperbolic stacking is
routinely applied for scanning velocity analysis in common-midpoint
stacking. Velocity transform inversion has proved to be a powerful
tool for data interpolation and amplitude-preserving multiple
supression Ji (1994a); Lumley et al. (1994); Thorson (1984).
Solving equation (81) for t0, we find that the asymptotic
inverse and adjoint operators have the elliptic summation path
| 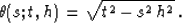 |
(82) |
The weighting functions of the asymptotic pseudo-unitary velocity
transform are found using formulas (34) and (35) to have the
form
| 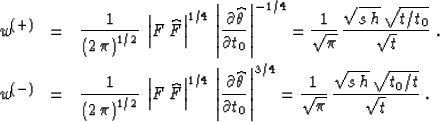 |
(83) |
| (84) |
The factor 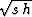 for pseudo-unitary velocity transform
weighting has been discovered empirically by Claerbout
.
for pseudo-unitary velocity transform
weighting has been discovered empirically by Claerbout
.





Next: Offset Continuation and DMO
Up: EXAMPLES
Previous: Post-Stack Residual Migration
Stanford Exploration Project
9/11/2000