Problem formulation

Mathematical interpolation theory considers a function f, defined on a regular grid N. The problem is to find f in a continuum, which includes N. I am not defining the dimensionality of N and f here because it is not essential for the derivations. Most of the examples in this paper use one-dimensional functions, but the general theory applies equally well to a higher number of dimensions. Furthermore, I am not specifying the exact meaning of "regular grid", since it will become clear from the further analysis. The function f is assumed to belong to a Hilbert space with a defined dot product.

If we restrict our consideration to a linear case, the desired solution will take the following general form  

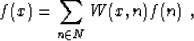$$f (x) = \sum_{n \in N} W (x, n) f (n)\;,$$ (1)

where x is a point from the continuum, and W (x, n) is a linear weight. If the grid N itself is considered as continuous, the sum in formula (1) transforms to an integral in dn. Two general properties of the linear weighting function W (x, n) are evident from formula (1).
 
Equality (2) is necessary to assure that the interpolation of a single spike at some point n does not change the value f (n) at the spike.
 
This property is the normalization condition. Formula (3) assures that interpolation of a constant function f(n) remains constant.

One classic example of the interpolation weight W (x, n) is the Lagrange polynomial, which has the form  

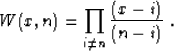$$W (x, n) = \prod_{i \neq n} \frac{(x-i)}{(n-i)}\;.$$ (2)

The Lagrange interpolation provides a unique polynomial, which goes exactly through the data points f (n). The known numerical instabilities of Lagrange's interpolation have been overcome by various types of spline interpolation de Boor (1978). It is curious to note that the interpolation and finite-difference filters, developed by Karrenbach (1995) from a general approach of self-similar operators, reduce to a localized form of Lagrange polynomials. The local 1-point Lagrange interpolation is equivalent to the nearest-neighbor interpolation, defined by the formula  

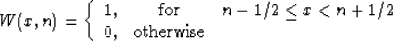$$W (x, n) = \left\{\begin{array} {lcr} 1, & \mbox{for} & n - 1/2 \leq x < n + 1/2 \ 0, & \mbox{otherwise} &\end{array}\right.$$ (3)

Likewise, the local 2-point Lagrange interpolation is equivalent to the linear interpolation, defined by the formula  

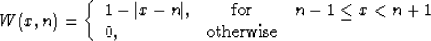$$W (x, n) = \left\{\begin{array} {lcr} 1 - \vert x-n\vert, &... ...- 1 \leq x < n + 1 \ 0, & \mbox{otherwise} &\end{array}\right.$$ (4)

The Lagrange interpolators of higher order correspond to more complicated polynomials.