![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) implements a generic 1-D
interpolation program. Analogous modules also exist for the 2-D and
3-D cases. The module includes the initialization (constructor)
subroutine interp1_init, which takes an array coord
to define the data coordinates and the SEPlib-style values
o1, d1, and n1 to define the model grid.
Additionally, it accepts an external function interp to
compute the interpolation filter W (x,n). The size of the filter is
defined by the integer parameter nfilt. An example of a
function with the interface of interp is lagrange
implements a generic 1-D
interpolation program. Analogous modules also exist for the 2-D and
3-D cases. The module includes the initialization (constructor)
subroutine interp1_init, which takes an array coord
to define the data coordinates and the SEPlib-style values
o1, d1, and n1 to define the model grid.
Additionally, it accepts an external function interp to
compute the interpolation filter W (x,n). The size of the filter is
defined by the integer parameter nfilt. An example of a
function with the interface of interp is lagrange
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which implements the local Lagrange
interpolation
, which implements the local Lagrange
interpolation![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) . The
initialization program allocates and computes three private
arrays: the integer array x that defines the mapping from the
data coordinates to the model grid, the logical array m that
masks the data values outside the grid, and the real-value array
w that stores coefficients of the interpolation filter.
Computing these arrays outside the actual interpolation program
interp1_op not only complies with the object-oriented design
of linear operators Fomel and Claerbout (1996), but also significantly
improves the efficiency when the interpolation operator is applied
more than once (e.g., in iterative least-square optimization.) The
arrays are deallocated by the ``destructor'' program
interp1_close.
. The
initialization program allocates and computes three private
arrays: the integer array x that defines the mapping from the
data coordinates to the model grid, the logical array m that
masks the data values outside the grid, and the real-value array
w that stores coefficients of the interpolation filter.
Computing these arrays outside the actual interpolation program
interp1_op not only complies with the object-oriented design
of linear operators Fomel and Claerbout (1996), but also significantly
improves the efficiency when the interpolation operator is applied
more than once (e.g., in iterative least-square optimization.) The
arrays are deallocated by the ``destructor'' program
interp1_close.
integer :: i, j, nf
real :: f, xi
nf = size (w)
do i = 1, nf
f = 1.
xi = x + 1. - i
do j = 1, nf
if (i /= j) f = f * (1. + xi / (i - j))
end do
w (i) = f
end do
stat = 0
end function lagrange
function lagrange (x, w) result (stat)
integer :: stat
real, intent (in) :: x
real, dimension (:) :: w
contains
subroutine interp1_init (coord, o1, d1, n1, interp, nfilt)
real, dimension (:), intent (in) :: coord
real, intent (in) :: o1, d1
integer, intent (in) :: n1, nfilt
interface
integer function interp (x, w)
real, intent (in) :: x
real, dimension (:) :: w
end function interp
end interface
integer :: id, ix, stat
real :: rx
nd = size (coord) ; nf = nfilt
if (.not. allocated (x)) allocate (x (nd), m (nd), w (nf,nd))
do id = 1, nd ; rx = (coord (id) - o1)/d1 ; ix = rx
rx = rx - ix ; x (id) = ix + 1 - 0.5*nf
m (id) = .true. ; w (:, id) = 0.
if ((x (id) + 1 >= 1) .and. (x (id) + nf <= n1)) then
m (id) = .false. ; stat = interp (rx, w (:,id))
end if
end do
end subroutine interp1_init
function interp1_op (adj, add, mod, ord) result (stat)
integer :: stat
logical, intent (in) :: adj, add
real, dimension (:) :: mod, ord
integer :: id, i1, i2
call adjnull (adj, add, mod, ord)
do id = 1, nd ; if (m (id)) cycle
i1 = x (id) + 1 ; i2 = x (id) + nf
if (adj) then
mod (i1:i2) = mod (i1:i2) + w (:,id) * ord (id)
else
ord (id) = sum (mod (i1:i2) * w (:,id)) + ord (id)
end if
end do
stat = 0
end function interp1_op
subroutine interp1_close ()
deallocate (x, m, w)
end subroutine interp1_close
end module interp1
module interp1
use adj_mod
integer, private :: nd, nf
integer, dimension (:), allocatable, private :: x
logical, dimension (:), allocatable, private :: m
real, dimension (:,:), allocatable, private :: w
To illustrate the forward interpolation operator, I chose a regularly
sampled chirp function ![]() as
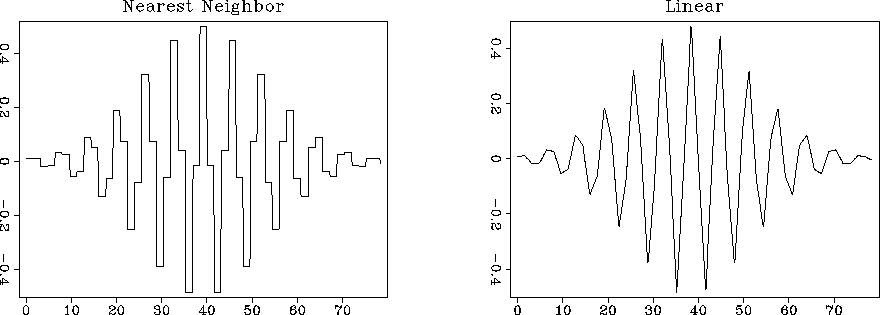
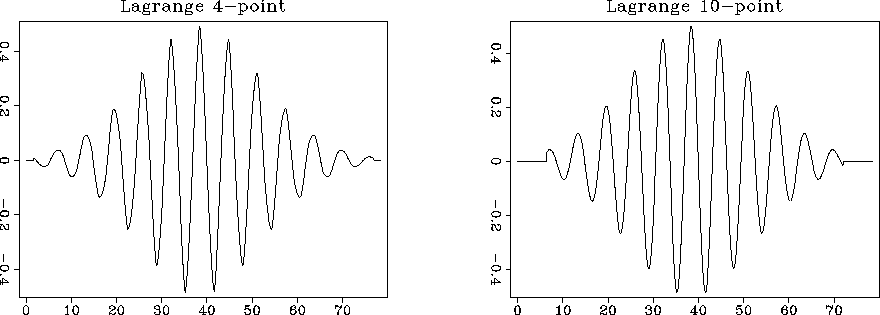
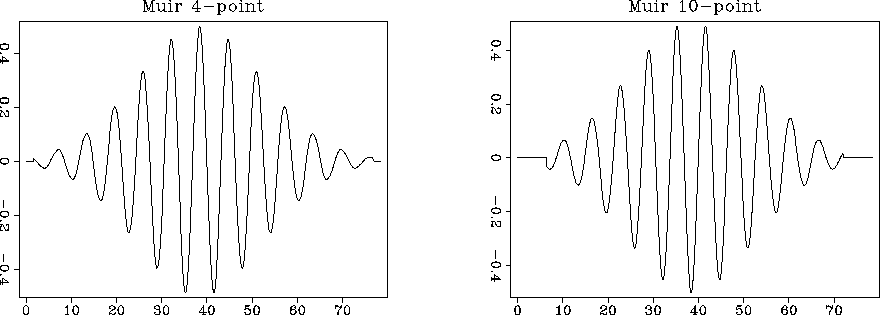
the input model (Figure 2). Figures 3,
4, and 5 show the result of forward
interpolation with different interpolators.
as
the input model (Figure 2). Figures 3,
4, and 5 show the result of forward
interpolation with different interpolators.
|
alias
Figure 2 The input is a regularly sampled chirp function. | 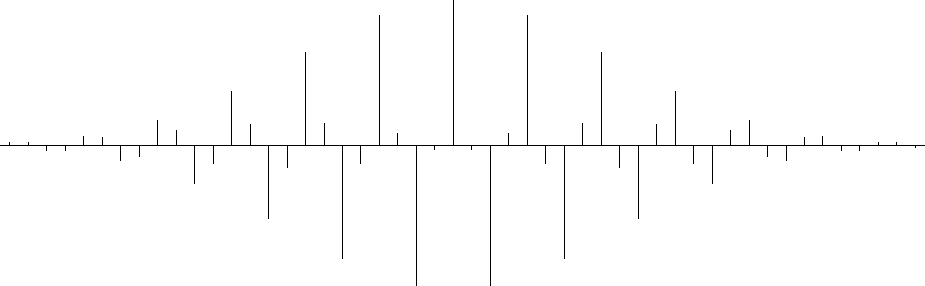 |
 |
 |
 |