The solutions to the focusing eikonal can be computed using current methods for solving the standard eikonal, either directly by modern eikonal solvers Fomel (1997); Sethian and Popovici (1997), or by ray tracing. We chose a ray tracing solution, because for reflection tomography is handier to have rays than traveltime maps.
To derive the ray-tracing system for the focusing eikonal
we begin by writing its associated Hamiltonian as
a function of the ray parameters ![]() and
and ![]() ,
,
| (10) |
The associated ray-tracing equation are:
![\begin{eqnarray}
\frac{d \xi}{d t}
=&
\;\;\frac{\partial H}{\partial p_\xi}
=&
...
...
p_{\tau}
\right)
\frac{\partial \sigma_f}{\partial \tau}
\right].\end{eqnarray}](img18.gif) |
||
| (11) |
Rays can be traced in ![]() by solving the ray-tracing equations
in (11)
by a standard ODE solver.
The appropriate initial conditions for
the ray parameters
by solving the ray-tracing equations
in (11)
by a standard ODE solver.
The appropriate initial conditions for
the ray parameters ![]() and
and ![]() when the source is at
when the source is at ![]() and the take-off angle is
and the take-off angle is ![]() are:
are:
![\begin{eqnarray}
p_{\tau_0}
&=&
\frac
{
\cos
\theta_\tau
}
{2}
\nonumber
\\ p_{\...
..._0\right)}
-
\sigma_f\left(\tau_0,\xi_0\right)
p_{\tau_0}
\right].\end{eqnarray}](img21.gif) |
||
| (12) |
To test the accuracy of our derivations we numerically
solved the ray tracing equations (11)
for a heterogeneous velocity function,
and compared the results with
a ray-tracing solution of the standard eikonal equation.
As expected, ![]() -rays map exactly into z-rays,
for all velocity fields.
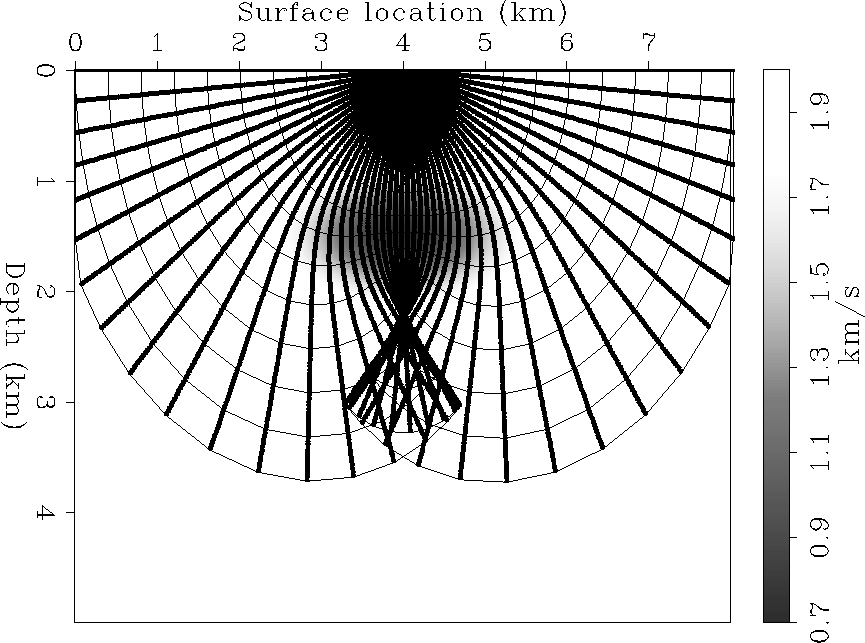
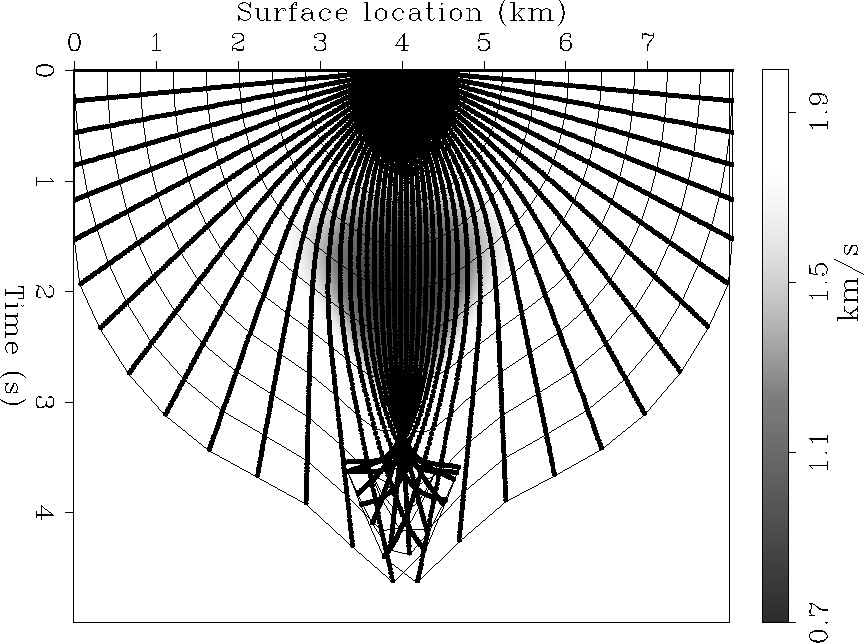
Figure 1 and
Figure 2
show an example of the ray field
when the velocity function is
a Gaussian-shaped negative velocity anomaly
superimposed onto a constant velocity background.
Notice that the focusing eikonal
handles correctly
the caustic and wavefront triplication
below the anomaly.
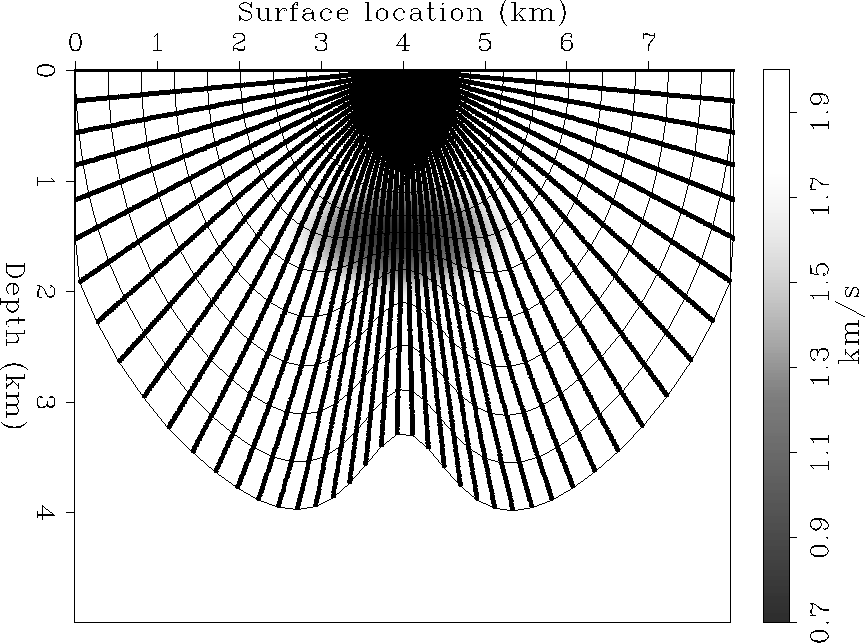
Figure 3 shows the effects
of neglecting the differential mapping factor
-rays map exactly into z-rays,
for all velocity fields.
Figure 1 and
Figure 2
show an example of the ray field
when the velocity function is
a Gaussian-shaped negative velocity anomaly
superimposed onto a constant velocity background.
Notice that the focusing eikonal
handles correctly
the caustic and wavefront triplication
below the anomaly.
Figure 3 shows the effects
of neglecting the differential mapping factor ![]() .It shows the
.It shows the ![]() -rays computed setting
-rays computed setting ![]() to zero, and remapped into
to zero, and remapped into ![]() .The wavefronts are distorted compared to the true wavefronts
shown in Figure 1
.The wavefronts are distorted compared to the true wavefronts
shown in Figure 1
 |
 |
 |