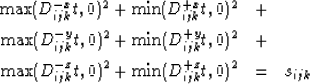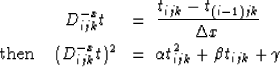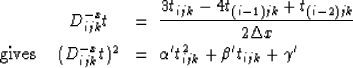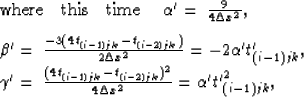Next: Accuracy
Up: Rickett & Fomel: Second-order
Previous: Introduction
Under a high frequency approximation, propagating wavefronts may be
described by the eikonal equation,
| 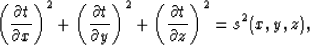 |
(1) |
where t is the traveltime, s is the slowness, and x, y and z
represent the spatial Cartesian coordinates.
The fast marching method solves equation (1) by
directly mimicking the advancing wavefront.
Every point on the computational
grid is classified into three groups:
points behind the wavefront, whose traveltimes are known and fixed;
points on the wavefront, whose traveltimes have been calculated, but
are not yet fixed; and points ahead of the wavefront.
The algorithm then proceeds as follows:
- 1.
- Choose the point on the wavefront with the smallest traveltime.
- 2.
- Fix this traveltime.
- 3.
- Advance the wavefront, so that this point is behind it, and
adjacent points are either on the wavefront or behind it.
- 4.
- Update traveltimes for adjacent points on the wavefront by
solving equation (1) numerically.
- 5.
- Repeat until every point is behind the wavefront.
The update procedure (step 4.) requires the solution of the following
quadratic equation for t,
| 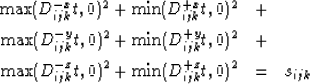 |
|
| |
| (2) |
where Dijk-x is a backward x difference operator at
grid point, ijk, Dijk+x is a forward x operator, and
finite-difference operators in y and z are defined similarly.
The roots of the quadratic equation, a t2 + b t + c = 0,
can be calculated explicitly as
| 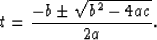 |
(3) |
Solving equation (2) amounts to accumulating
coefficients a, b and c from its non-zero terms, and evaluating
t with equation (3).
If we choose a two-point finite-difference operator, such as
| 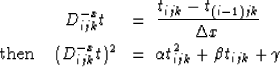 |
(4) |
| (5) |
where
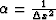 ,
,
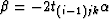 and
and
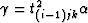 .Coefficients a, b and c can now be calculated from
.Coefficients a, b and c can now be calculated from
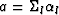 ,
,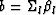 , and
, and
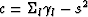 ,where the summation index, l, refers to the six terms in
equation (2) subject to the various min/max
conditions.
,where the summation index, l, refers to the six terms in
equation (2) subject to the various min/max
conditions.
This two-point stencil, however, is only accurate to first-order.
If instead we choose a suitable three-point finite-difference
stencil, we may expect the method to have second-order accuracy. For
example, the second-order upwind stencil,
| 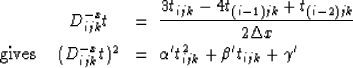 |
(6) |
| (7) |
Coefficients, a, b and c can be accumulated from 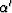 ,
,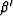 and
and 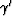 as before, and if the traveltime, t(i-2)jk
is not available, first-order values may be substituted.
as before, and if the traveltime, t(i-2)jk
is not available, first-order values may be substituted.





Next: Accuracy
Up: Rickett & Fomel: Second-order
Previous: Introduction
Stanford Exploration Project
5/1/2000