




Next: Conclusions
Up: Fomel & Claerbout: Implicit
Previous: Three-dimensional implicit velocity continuation
Can the constant-velocity result help us achieve the challenging goal
of a stable implicit depth extrapolation through media with lateral
velocity variations?
The first idea that comes to mind is to replace the space-invariant
helix filters with a precomputed set of spatially varying filters,
which reflect local changes in the velocity fields. This approach
would merely reproduce the conventional practice of explicit depth
extrapolators, popularized by Holberg (1988) and
Hale (1991b). However, it hides the danger of losing
the property of unconditional stability, which is obviously the major
asset of implicit extrapolators.
Another route, partially explored by Nichols (1991), is
to implement the matrix inversion in the three-dimensional implicit
scheme by an iterative method. In this case, the helix inversion may
serve as a powerful preconditioner, providing an immediate answer in
constant velocity layers and speeding up the convergence in the case
of velocity variations. To see why this might be true, one can write
the variable-coefficient matrix 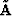 in the form
in the form
| 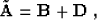 |
(19) |
where matrix 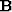 corresponds to some constant average velocity,
and
corresponds to some constant average velocity,
and 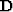 is the matrix of velocity perturbations. The system of
linear equations that we need to solve is then
is the matrix of velocity perturbations. The system of
linear equations that we need to solve is then
| 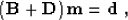 |
(20) |
where 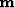 is the vector of extrapolated wavefield, and
is the vector of extrapolated wavefield, and
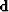 is an appropriate righthand side. The helix transform
provides us with the operator
is an appropriate righthand side. The helix transform
provides us with the operator 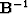 , which we can use to
precondition system (20). Introducing the change of
variables
, which we can use to
precondition system (20). Introducing the change of
variables
| 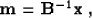 |
(21) |
we can transform the original system (20) to the form
| 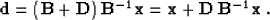 |
(22) |
When the velocity perturbation is small![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) , even
the simple iteration
, even
the simple iteration
| 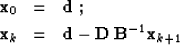 |
(23) |
| (24) |
will converge rapidly to the desired solution. This interesting
possibility needs thorough testing.
The third untested possibility (Papanicolaou, personal communication)
is to implement a clever patching in the velocity domain, applying a
constant-velocity filter locally inside each patch. Recently developed
fast wavelet transform techniques Vetterli and Kovacevic (1995), in particular the
local cosine transform , provide a formal framework for that
approach.





Next: Conclusions
Up: Fomel & Claerbout: Implicit
Previous: Three-dimensional implicit velocity continuation
Stanford Exploration Project
9/12/2000
![]() in the form
in the form
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) , even
the simple iteration
, even
the simple iteration