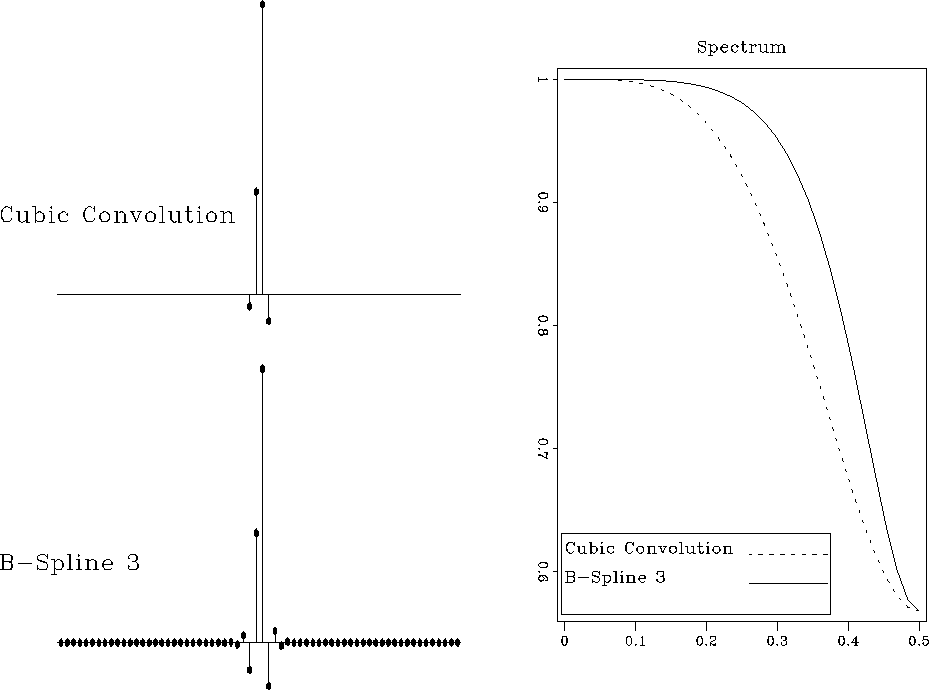Next: 2-D example
Up: Forward Interpolation
Previous: Interpolation and convolution
B-splines represent a particular example of a convolutional basis.
Because of their compact support and other attractive numerical
properties, B-splines are a good basis choice for the forward
interpolation problem and related signal processing problems Unser (1999).
B-splines of the order 0 and 1 coincide with the nearest neighbor and
linear interpolants (2) and (3) respectively.
B-splines 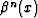 of a higher order n can be defined by a
repetitive convolution of the zeroth-order spline
of a higher order n can be defined by a
repetitive convolution of the zeroth-order spline 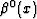 (the
box function) with itself:
(the
box function) with itself:
| 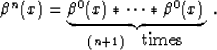 |
(10) |
There is also the explicit expression
| 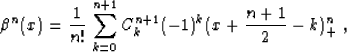 |
(11) |
which can be proved by induction. Here Ckn+1 are the binomial
coefficients, and the function x+ is defined as follows:
| 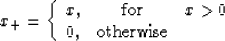 |
(12) |
As follows from formula (11), the most commonly used cubic
B-spline 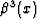 has the expression
has the expression
| 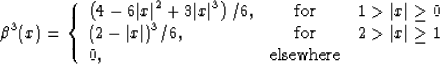 |
(13) |
The corresponding discrete filter 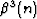 is a centered 3-point
filter with coefficients 1/6, 2/3, and 1/6. According to the
traditional method, a deconvolution with this filter is performed as a
tridiagonal matrix inversion de Boor (1978). One can accomplish it more
efficiently by spectral factorization and recursive filtering
Unser et al. (1993a). The recursive filtering approach generalizes
straightforwardly to B-splines of higher orders.
is a centered 3-point
filter with coefficients 1/6, 2/3, and 1/6. According to the
traditional method, a deconvolution with this filter is performed as a
tridiagonal matrix inversion de Boor (1978). One can accomplish it more
efficiently by spectral factorization and recursive filtering
Unser et al. (1993a). The recursive filtering approach generalizes
straightforwardly to B-splines of higher orders.
Both the support length and the smoothness of B-splines increase with
the order. In the limit, B-slines converge to the Gaussian function.
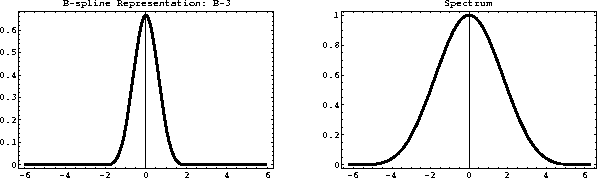
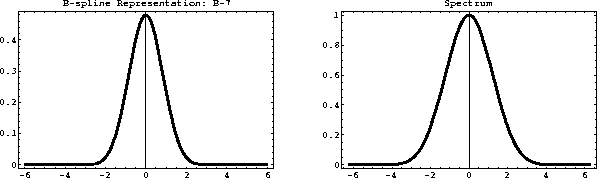
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the third- and
seventh-order splines
show the third- and
seventh-order splines 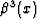 and
and 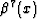 and their
continuous spectra.
and their
continuous spectra.
splint3
Figure 11 Third-order B-spline 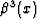 (left)
and its spectrum (right).
(left)
and its spectrum (right).




 splint7
splint7
Figure 12 Seventh-order B-spline 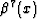 (left)
and its spectrum (right).
(left)
and its spectrum (right).





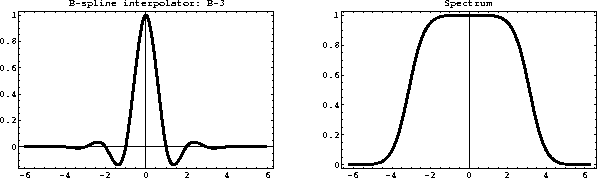
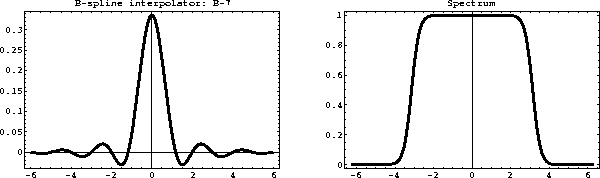
It is important to realize the difference between B-splines and the
corresponding interpolants W(x,n), which are sometimes called
cardinal splines . An explicit computation of the cardinal
splines is impractical, because they have infinitely long support.
Typically, they are constructed implicitly by the two-step
interpolation method, outlined in the previous subsection. The
cardinal splines of orders 3 and 7 and their spectra are shown in
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . As B-splines converge
to the Gaussian function, the corresponding interpolants rapidly
converge to the sinc function (4). A good convergence
is achieved with the help of the infinitely long support, which
results from recursive filtering at the first step of the
interpolation procedure.
. As B-splines converge
to the Gaussian function, the corresponding interpolants rapidly
converge to the sinc function (4). A good convergence
is achieved with the help of the infinitely long support, which
results from recursive filtering at the first step of the
interpolation procedure.
crdint3
Figure 13 Effective third-order B-spline interpolant
(left) and its spectrum (right).




 crdint7
crdint7
Figure 14 Effective seventh-order B-spline interpolant
(left) and its spectrum (right).





In practice, the recursive filtering step adds only marginally to the
total interpolation cost. Therefore, an n-th order B-spline
interpolation is comparable in cost with any other method with an
(n+1)-point interpolant. The comparison in accuracy usually turns
out in favor of B-splines. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare interpolation errors of B-splines and
other similar-cost methods on the example from Figure
compare interpolation errors of B-splines and
other similar-cost methods on the example from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
cubspl
Figure 15 Interpolation error of the cubic
convolution interpolant (dashed line) compared to that of the
third-order B-spline (solid line).
|
| 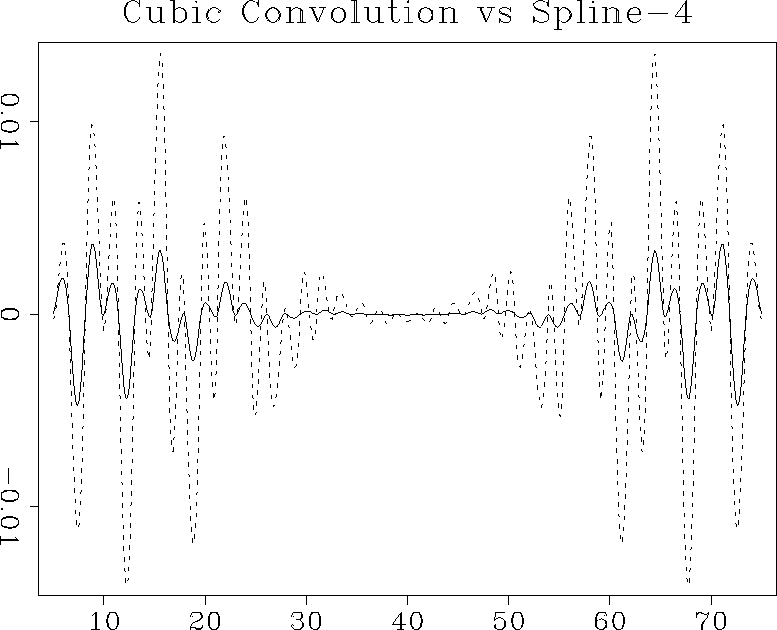 |





kaispl
Figure 16 Interpolation error of the 8-point
windowed sinc interpolant (dashed line) compared to that of the
seventh-order B-spline (solid line).
|
| 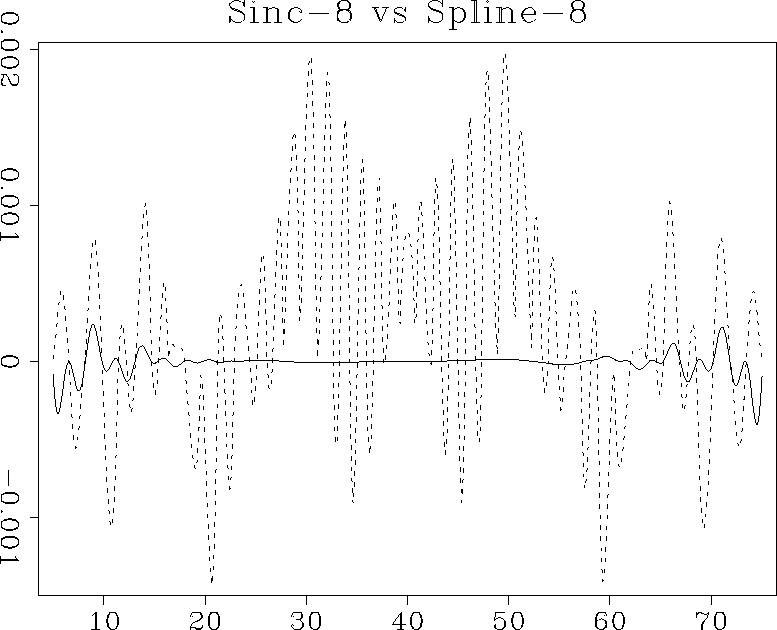 |





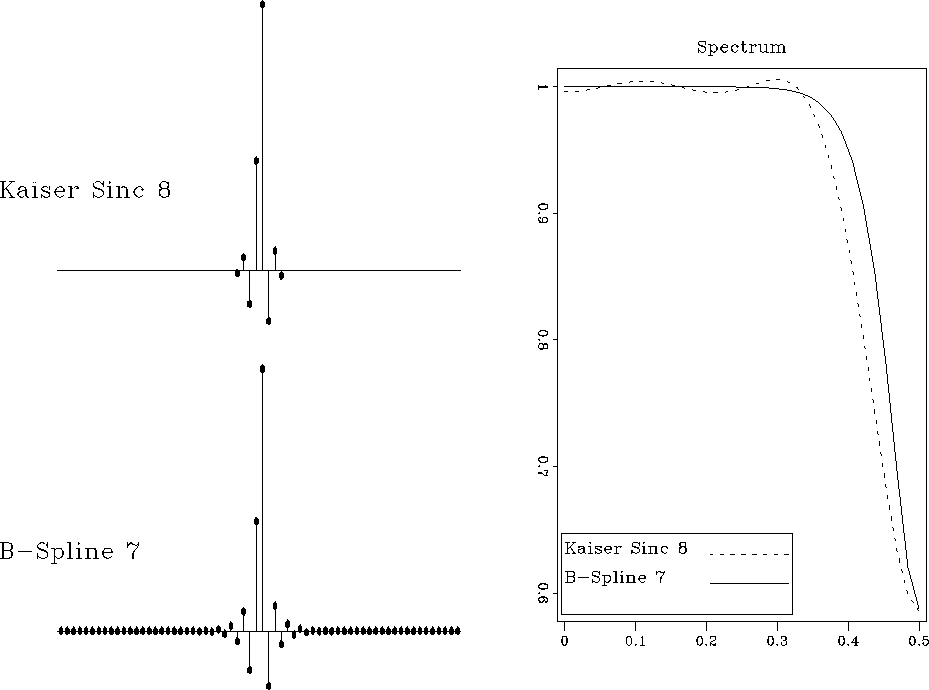
Similarly to Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we
can also compare the discrete responses of B-spline interpolation with
those of other methods. The right plots in
Figures
, we
can also compare the discrete responses of B-spline interpolation with
those of other methods. The right plots in
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show that the
discrete spectra of the effective B-spline interpolants are genuinely
flat at low frequencies and wider than those of the competitive
methods. Although the B-spline responses are infinitely long because
of the recursive filtering step, they exhibit a fast amplitude decay.
show that the
discrete spectra of the effective B-spline interpolants are genuinely
flat at low frequencies and wider than those of the competitive
methods. Although the B-spline responses are infinitely long because
of the recursive filtering step, they exhibit a fast amplitude decay.
speccubspl
Figure 17 Discrete interpolation responses
of cubic convolution and third-order B-spline interpolants (left)
and their discrete spectra (right) for x=0.7.
|
| 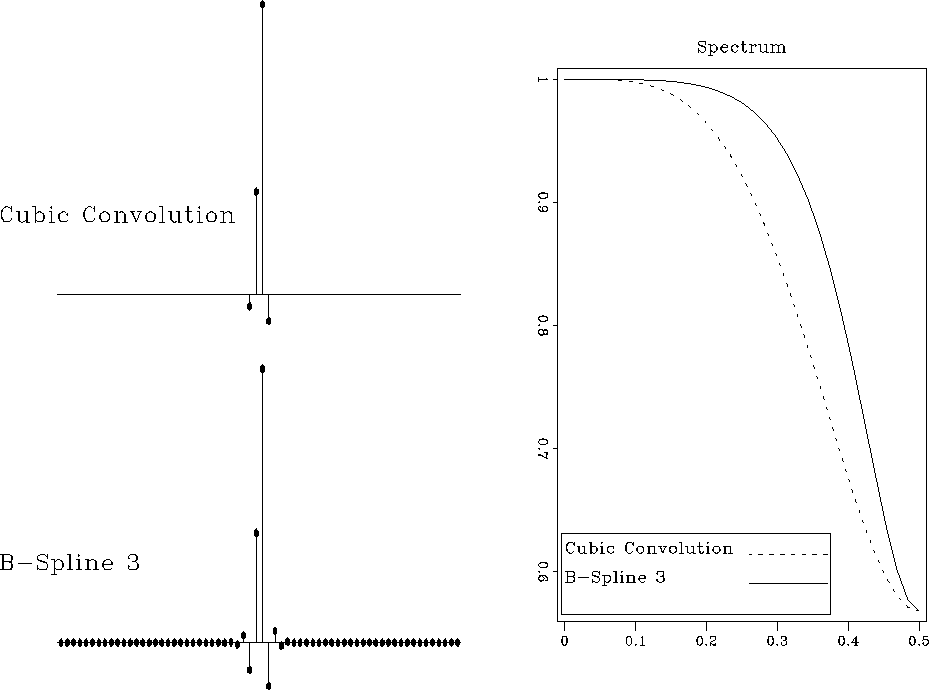 |





speckaispl
Figure 18 Discrete interpolation responses of
8-point windowed sinc and seventh-order B-spline interpolants (left)
and their discrete spectra (right) for x=0.7.
|
|  |










Next: 2-D example
Up: Forward Interpolation
Previous: Interpolation and convolution
Stanford Exploration Project
11/9/2000
![]() of a higher order n can be defined by a
repetitive convolution of the zeroth-order spline
of a higher order n can be defined by a
repetitive convolution of the zeroth-order spline ![]() (the
box function) with itself:
(the
box function) with itself:
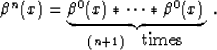
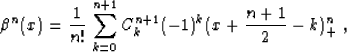
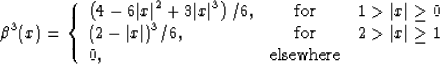
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the third- and
seventh-order splines
show the third- and
seventh-order splines ![]() and
and ![]() and their
continuous spectra.
and their
continuous spectra.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . As B-splines converge
to the Gaussian function, the corresponding interpolants rapidly
converge to the sinc function (4). A good convergence
is achieved with the help of the infinitely long support, which
results from recursive filtering at the first step of the
interpolation procedure.
. As B-splines converge
to the Gaussian function, the corresponding interpolants rapidly
converge to the sinc function (4). A good convergence
is achieved with the help of the infinitely long support, which
results from recursive filtering at the first step of the
interpolation procedure.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare interpolation errors of B-splines and
other similar-cost methods on the example from Figure
compare interpolation errors of B-splines and
other similar-cost methods on the example from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
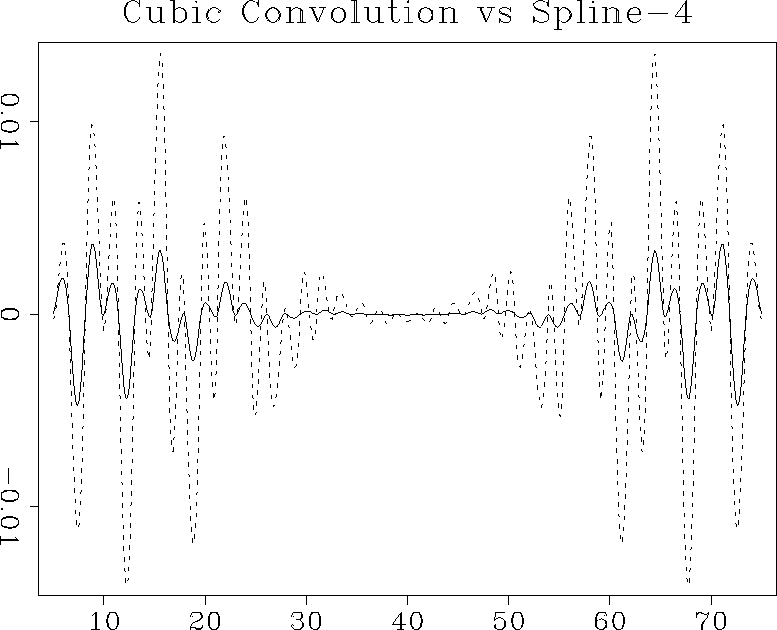
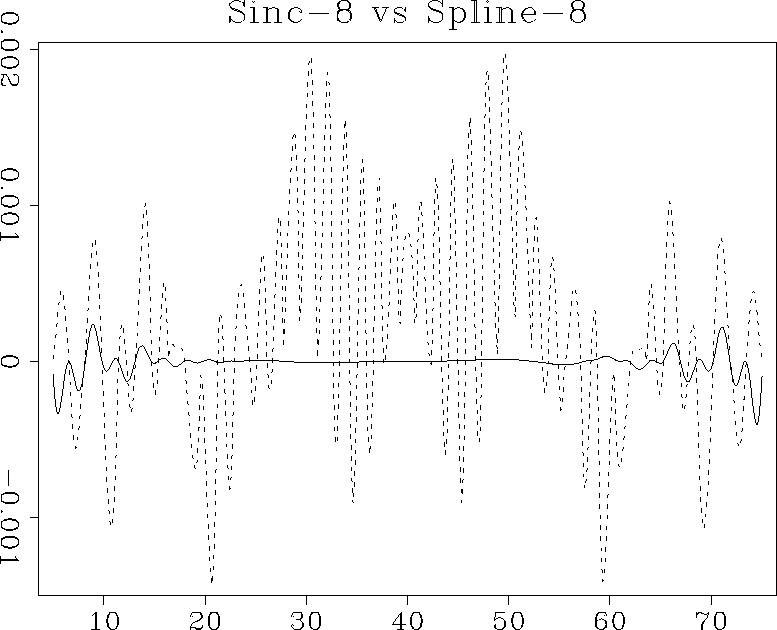
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we
can also compare the discrete responses of B-spline interpolation with
those of other methods. The right plots in
Figures
, we
can also compare the discrete responses of B-spline interpolation with
those of other methods. The right plots in
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show that the
discrete spectra of the effective B-spline interpolants are genuinely
flat at low frequencies and wider than those of the competitive
methods. Although the B-spline responses are infinitely long because
of the recursive filtering step, they exhibit a fast amplitude decay.
show that the
discrete spectra of the effective B-spline interpolants are genuinely
flat at low frequencies and wider than those of the competitive
methods. Although the B-spline responses are infinitely long because
of the recursive filtering step, they exhibit a fast amplitude decay.