




Next: Linearized approximations
Up: Alkhalifah and Fomel: Anisotropy
Previous: REFERENCES
The chain rule of differentiation leads to the equality
| 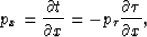 |
(24) |
where 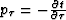 . It is
convenient to transform equality (A-1) to the form
. It is
convenient to transform equality (A-1) to the form
| 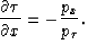 |
(25) |
Using the expression for 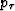 from the main text, we can
write equation (A-2) as a quadratic polynomial in px2
as follows
from the main text, we can
write equation (A-2) as a quadratic polynomial in px2
as follows
where
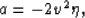
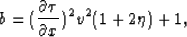
and
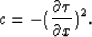
Since  can be small (as small as zero for isotropic media),
we use the following form of solution to the quadratic equation
can be small (as small as zero for isotropic media),
we use the following form of solution to the quadratic equation
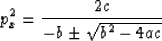
Press et al. (1992). This form does not go to infinity as  approaches
. We choose the solution with the negative sign in front of the
square root, because this solution complies with the isotropic result
when
approaches
. We choose the solution with the negative sign in front of the
square root, because this solution complies with the isotropic result
when  is equal to zero.
is equal to zero.





Next: Linearized approximations
Up: Alkhalifah and Fomel: Anisotropy
Previous: REFERENCES
Stanford Exploration Project
9/12/2000
![]() from the main text, we can
write equation (A-2) as a quadratic polynomial in px2
as follows
from the main text, we can
write equation (A-2) as a quadratic polynomial in px2
as follows
![]()
![]()
![]()
![]() can be small (as small as zero for isotropic media),
we use the following form of solution to the quadratic equation
can be small (as small as zero for isotropic media),
we use the following form of solution to the quadratic equation
![]()