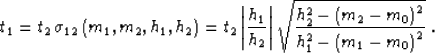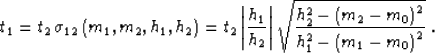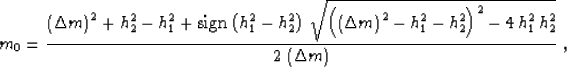Next: AMO APERTURE: CASCADING MIGRATION
Up: DERIVING AMO AS A
Previous: DERIVING AMO AS A
When the input-offset vector 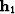 is parallel
to the output-offset vector
is parallel
to the output-offset vector 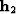 ,
the triangle
,
the triangle 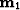 -
-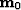 -
-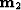 , formed
by the midpoints of the input trace, zero-offset trace, and output
trace, degenerates to a line. The location of the zero-offset midpoint
, formed
by the midpoints of the input trace, zero-offset trace, and output
trace, degenerates to a line. The location of the zero-offset midpoint
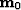 is not constrained by the input and output midpoints and can
take different values on the line. The cascade of DMO and inverse DMO
becomes a convolution on that line. To find the summation path of 2-D
AMO (offset continuation), one needs to consider the envelope of the
family of traveltime curves (where m0 is the parameter of a
curve in the family):
is not constrained by the input and output midpoints and can
take different values on the line. The cascade of DMO and inverse DMO
becomes a convolution on that line. To find the summation path of 2-D
AMO (offset continuation), one needs to consider the envelope of the
family of traveltime curves (where m0 is the parameter of a
curve in the family):
| 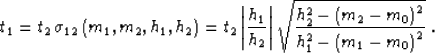 |
(49) |
Solving the envelope condition
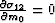 for the zero-offset midpoint m0 produces
for the zero-offset midpoint m0 produces
| 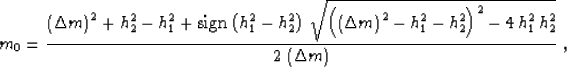 |
(50) |
where 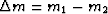 . Substituting (51)
into (50), we obtain the explicit
expression (3) of the offset continuation summation
path.
C
. Substituting (51)
into (50), we obtain the explicit
expression (3) of the offset continuation summation
path.
C





Next: AMO APERTURE: CASCADING MIGRATION
Up: DERIVING AMO AS A
Previous: DERIVING AMO AS A
Stanford Exploration Project
6/14/2000