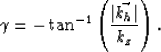Next: Regularization of the angle
Up: Sava & Fomel: Angle-gathers
Previous: Introduction
The Fourier-domain stretch represented by equation (1) is equivalent to a slant stack in the 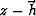 domain. Indeed, we can convert an image gather in the offset-domain (
domain. Indeed, we can convert an image gather in the offset-domain (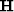 ) to one in the angle-domain (
) to one in the angle-domain (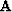 ), using a slant-stack equation of the form
), using a slant-stack equation of the form
| 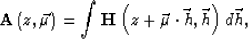 |
(2) |
where 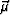 is a vector describing the direction of the stack.
is a vector describing the direction of the stack.
Fourier transforming equation (2) over the depth
axis, we obtain
![\begin{displaymath}
\underline {\bf A}\left (k_z,\vec \mu\right ) = \int\left [\int \H{z+\vec \mu\cdot\vec h}{\vec h} d\vec h\right ]e^{i k_zz} dz\end{displaymath}](img10.gif)
where the underline stands for a 1-D Fourier transform. We can continue by writing the equation
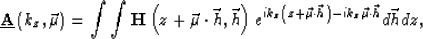
where we can re-arrange the terms as
![\begin{displaymath}
\underline {\bf A}\left (k_z,\vec \mu\right ) = \int \left [...
...t\vec h\right )} dz\right ]e^{-ik_z\vec \mu\cdot\vec h}d\vec h,\end{displaymath}](img12.gif)
which highlights the relation between the 1-D Fourier-transformed angle-domain and offset-domain representation of the seismic images:
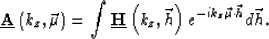
We recognize on the right-hand side of the previous equation additional Fourier transforms over the offset axes, and therefore we can write

where the triple underline stands for the 3-D Fourier transform of the
offset-domain common-image gather. Finally, defining 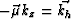 , we
can conclude that the 1-D Fourier transforms of angle-domain gathers
are equivalent to the 3-D Fourier transforms of the offset-domain
gathers,
, we
can conclude that the 1-D Fourier transforms of angle-domain gathers
are equivalent to the 3-D Fourier transforms of the offset-domain
gathers,
| 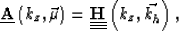 |
(3) |
subject to the stretch of the offset axis according to the simple law
| 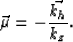 |
(4) |
We can recognize in equation (4) the fundamental relation between the reflection angle and the Fourier-domain quantities that are evaluated in wave-equation migration. This equation also shows that the angles evaluated by (1) are indeed equivalent to slant stacks on offset-domain
common-image gathers. Therefore, we could either compute angles for each of the two offset axes with the equations
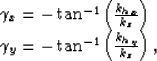
or compute one angle corresponding to the entire offset vector:
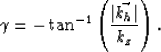





Next: Regularization of the angle
Up: Sava & Fomel: Angle-gathers
Previous: Introduction
Stanford Exploration Project
5/1/2000
![]()
![]()
![]()
![]()
![]()