I implemented a finite-difference simulator for the rudimentary acoustic two-way wave equation 10. For my preliminary exploits, I chose a 2-D plane. The finite difference simulator computes the wavefield for arbitrarily placed sources. I intend to first model simple transmission experiments, possibly with plane waves. Seismogramms for various acquisition geometries are easily extracted from the complete wavefield.
Following Gassmann's model, the fluid saturated, porous rock properties enter the simulator by defining the velocity field v of equation 11. In particular, Gassmann's bulk modulo and density depend on the fluid saturation So, Sw and Sg. I assume that the fluid flow in a producing reservoir and the wave propagation of a seismic experiment are decoupled, since both processes happen on very different time scales and are limited to small, linear motions. Consequently, I assume the saturation and the dependent velocity as fixed during a seismic experiment. However, I expect that the saturation and consequently the velocity of the reservoir rocks possibly changes between subsequent experiments.
I implemented the finite difference simulator as part of Jest Schwab and Schroeder (1997), a Java inversion library. The linear simulators contain their adjoint operator that are checked by the dot product test.
Finite difference wave equation. I implement the acoustic scalar wave equation
| |
(18) |
![]()
| |
(19) |
Boundary conditions. I also implemented Clayton and Engquist's 1980 absorbing boundary conditions. The absorption of the wave is due to a subtle change of the material coefficients at all edge points of the computational grid. While the interior coefficients implement the two-way wave equation, the boundary points implement the paraxial one-way wave equation. The one-way wave equation propagates the energy outwards but not inwards. Unfortunately, I am currently baffled since my implementation does not absorb the energy as promised.
 |
Stability analysis. The fundamental solution to the difference equation above is
| (20) |
| (21) |
![]()
![]()
![]()
Implementation.
The finite difference equation 19
expresses a recursive computation in time
of the wavefield ![]() over time:
over time:
| |
(22) |
Figure 5 indicates how the algorithm recursively computes the values in the red plane from the earlier green and blue plane. The first two time planes implement the initial conditions. Once the entire cube is computed, a constant time plane contains a snapshots of the wavefield. The extraction of all wavefield values that correspond to a (x,y)-location yields a time dependent seismogram.
|
cube
Figure 5 Computational grid. The domain and range of the finite difference implementation is an identical cube of (x,y,t) values. The input cube contains the source amplitudes of any point in time and space. The output cube contains the wavefield amplitude of any point in time and space. The values in the red plane are computed from the values of the green and blue plane according to the difference equation 19. | 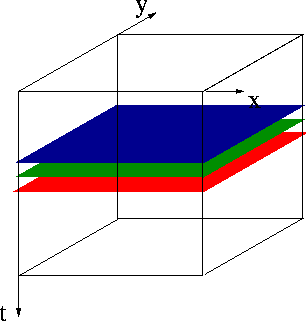 |
The recursion 22 is a handy approach to compute
the wave solution ![]() of the fundamental operator equation
of the fundamental operator equation
| |
(23) |
Because of the operator's recursive definition,
we do not know its explicit matrix form ![]() .
However,
the recursion 22 is easily reformulated to
.
However,
the recursion 22 is easily reformulated to
![]()
![\begin{displaymath}
\left[
\begin{array}
{c}
s_0 \\ s_1 \\ s_2 \\ s_3 \\ \end{ar...
...ma_0 \\ \sigma_1 \\ \sigma_2 \\ \sigma_3 \\ \end{array}\right].\end{displaymath}](img75.gif) |
(24) |
How do we find an expression for the adjoint of ![]() ?
Since
?
Since
![]() ,
we yield an explicit expression for
the inverse of the adjoint of
,
we yield an explicit expression for
the inverse of the adjoint of ![]() from 24:
from 24:
![\begin{displaymath}
\left[
\begin{array}
{c}
\sigma_0 \\ \sigma_1 \\ \sigma_2 \\...
...gin{array}
{c}
s_0 \\ s_1 \\ s_2 \\ s_3 \\ \end{array}\right]. \end{displaymath}](img78.gif)
![]()
![]()