A nonlinear-estimation method

What I have described above represents my first iteration. It can be called a ``linear-estimation method." Next we will try a ``nonlinear-estimation method" and see that it works better. If we think of minimizing the relative error in the residual, then in linear estimation we used the wrong divisor--that is, we used the squared data v² where we should have used the squared residual $(v - \alpha h)^2$.Using the wrong divisor is roughly justified when the crosstalk $\alpha$ is small because then v² and $(v - \alpha h)^2$are about the same. Also, at the outset the residual was unknown, so we had no apparent alternative to v², at least until we found $\alpha$.Having found the residual, we can now use it in a second iteration. A second iteration causes $\alpha$ to change a bit, so we can try again. I found that, using the same data as in Figure 1, the sequence of iterations converged in about two iterations.

 

reswait
Figure 2 Comparison of weighting methods. Left shows crosstalk as badly removed by uniformly weighted least squares. Middle shows crosstalk removed by deriving a weighting function from the input data. Right shows crosstalk removed by deriving a weighting function from the fitting residual. Press button for movie over iterations.

Figure 2 shows the results of the various weighting methods. Mathematical equations summarizing the bottom row of this figure are:

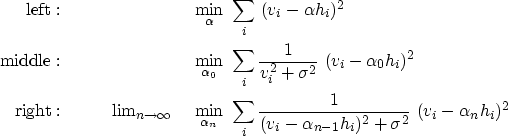$$\begin{eqnarray} {\rm left}:\quad\quad&& \min_\alpha \ \sum_i \ (v_i-\alpha h_i... ...\over (v_i-\alpha_{n-1}h_i)^2 + \sigma^2} \ (v_i-\alpha_n h_i)^2\end{eqnarray}$$ (9) (10) (11)

For the top row of the figure, these equations also apply, but $\bold v$ and $\bold h$ should be swapped.