Prediction-error filters on synthetic data

The idea of using a gap in a prediction filter is to relax the goal of converting realistic signals into perfect impulses. Figure 7 shows synthetic data, sparse noise into a leaky integrator, and deconvolutions with prediction-error filters.

 

dleak
Figure 7 Deconvolution of leaky integrator signals with PE filters of various prediction-gap sizes. Inputs and outputs on alternate traces. Gap size increases from left to right.

Theoretically, the filters should turn out to be $1-(.9Z)^{\rm gap}$.Varying degrees of success are achieved by the filters obtained on the different traces, but overall, the results are good.

To see what happens when an unrealistic deconvolution goal is set for prediction error, we can try to compress a wavelet that is resistant to compression--for example, the impulse response of a Butterworth bandpass filter. The perfect filter to compress any wavelet is its inverse. But a wide region of the spectrum of a Butterworth filter is nearly zero, so any presumed inverse must require nearly dividing by that range of zeros. Compressing a Butterworth filter is so difficult that I omitted the random numbers used in Figure 7 and applied prediction error to the Butterworth response itself, in Figure 8.

 

dbutter Figure 8 Butterworth deconvolution by prediction error.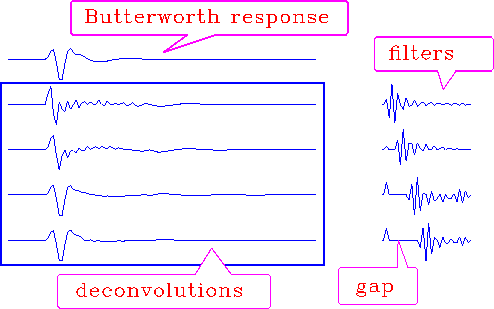

Thus, we have seen that gapped PE filters sometimes are able to compress a wavelet, and sometimes are not. In real life, resonances arise in the earth's shallow layers; and as we will see, the resonant filters can be shortened by PE filters.