




Next: FT OF RANDOM NUMBERS
Up: My rise-time proof of
Previous: My rise-time proof of
Although the Z-transform method
is a great aid in studying cases
where divergence (as 1/t) plays a role,
it has the disadvantage that it destroys the formal interchangeability
between the time domain and the frequency domain.
To take advantage of the analytic simplicity
of the Z-transform,
we consider instead the dual to the rise-time problem.
Instead of a signal
whose square vanishes at negative time, we have a spectrum
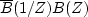 that vanishes at negative frequencies.
We measure how fast this spectrum can rise after
that vanishes at negative frequencies.
We measure how fast this spectrum can rise after 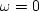 .We will find this time interval to
be related to the time duration
.We will find this time interval to
be related to the time duration 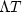 of the complex-valued signal bt.
More precisely, we now define the lowest significant frequency
component
of the complex-valued signal bt.
More precisely, we now define the lowest significant frequency
component 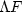 in the spectrum, analogously to
(3), as
in the spectrum, analogously to
(3), as
| 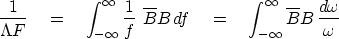 |
(4) |
where we have assumed the spectrum is normalized,
i.e., the zero lag of the auto-correlation of bt is unity.
Now recall the bilinear transform,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which represents
), which represents 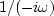 as
the coefficients of
as
the coefficients of 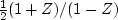 , namely,
, namely,
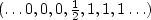 .
.
The pole right on the unit circle at Z = 1 causes some nonuniqueness.
Because 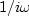 is an imaginary, odd, frequency function,
we will want an odd expression
(such as on page
is an imaginary, odd, frequency function,
we will want an odd expression
(such as on page ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
to insert into (4):
)
to insert into (4):
| 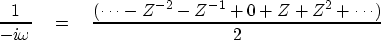 |
(5) |
Using limits on the integrals for time-sampled functions and
inserting (5) into (4) gives
| 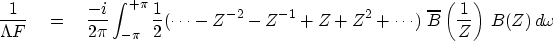 |
(6) |
Let st be the autocorrelation of bt.
Since any integral around the unit circle
of a Z-transform polynomial selects
the coefficient of Z0 of its integrand, we have
| 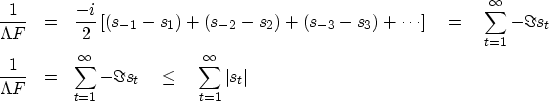 |
(7) |
| (8) |
The height of the autocorrelation has been normalized to s0=1.
The sum in (8) is an integral representing area under the
|st| function.
So the area is a measure of the autocorrelation width
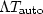 .Thus,
.Thus,
| 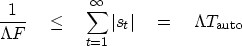 |
(9) |
Finally, we must relate the duration of a signal 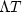 to the
duration of its autocorrelation
to the
duration of its autocorrelation 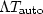 .Generally speaking,
it is easy to find a long signal that has short autocorrelation.
Just take an arbitrary short signal
and convolve it using a lengthy all-pass filter.
Conversely, we cannot get a long autocorrelation function
from a short signal.
A good example is the autocorrelation of a rectangle function,
which is a triangle.
The triangle appears to be twice as long,
but considering that the triangle tapers down,
it is reasonable to assert that the
.Generally speaking,
it is easy to find a long signal that has short autocorrelation.
Just take an arbitrary short signal
and convolve it using a lengthy all-pass filter.
Conversely, we cannot get a long autocorrelation function
from a short signal.
A good example is the autocorrelation of a rectangle function,
which is a triangle.
The triangle appears to be twice as long,
but considering that the triangle tapers down,
it is reasonable to assert that the 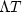 's are the same.
Thus, we conclude that
's are the same.
Thus, we conclude that
| 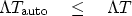 |
(10) |
Inserting this inequality into (9),
we have the uncertainty relation
| 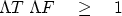 |
(11) |
Looking back over the proof, I feel that the basic
time-bandwidth idea is in the equality (7).
I regret that the verbalization of this idea, boxed following,
is not especially enlightening.
The inequality arises from
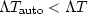 ,which is a simple idea.
,which is a simple idea.
|
The inverse moment of the normalized spectrum of an analytic signal
equals the imaginary part of the mean of its autocorrelation.
|
EXERCISES:
-
Consider B(Z) = [1 - (Z/Z0)n]/(1 -Z/Z0) as Z0 goes to
the unit circle.
Sketch the signal and its squared amplitude.
Sketch the frequency function and its squared amplitude.
Choose
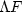 and
and 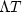 .
. -
A time series made up of two frequencies can be written as
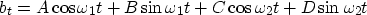
Given 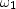 ,
, 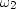 , b0, b1, b2, and b3,
show how to calculate
the amplitude and phase angles of the two sinusoidal components.
, b0, b1, b2, and b3,
show how to calculate
the amplitude and phase angles of the two sinusoidal components.





Next: FT OF RANDOM NUMBERS
Up: My rise-time proof of
Previous: My rise-time proof of
Stanford Exploration Project
10/21/1998
![]() that vanishes at negative frequencies.
We measure how fast this spectrum can rise after
that vanishes at negative frequencies.
We measure how fast this spectrum can rise after ![]() .We will find this time interval to
be related to the time duration
.We will find this time interval to
be related to the time duration ![]() of the complex-valued signal bt.
More precisely, we now define the lowest significant frequency
component
of the complex-valued signal bt.
More precisely, we now define the lowest significant frequency
component ![]() in the spectrum, analogously to
(3), as
in the spectrum, analogously to
(3), as
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which represents
), which represents ![]() is an imaginary, odd, frequency function,
we will want an odd expression
(such as on page
is an imaginary, odd, frequency function,
we will want an odd expression
(such as on page ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
to insert into (4):
)
to insert into (4):
![]() to the
duration of its autocorrelation
to the
duration of its autocorrelation ![]() .Generally speaking,
it is easy to find a long signal that has short autocorrelation.
Just take an arbitrary short signal
and convolve it using a lengthy all-pass filter.
Conversely, we cannot get a long autocorrelation function
from a short signal.
A good example is the autocorrelation of a rectangle function,
which is a triangle.
The triangle appears to be twice as long,
but considering that the triangle tapers down,
it is reasonable to assert that the
.Generally speaking,
it is easy to find a long signal that has short autocorrelation.
Just take an arbitrary short signal
and convolve it using a lengthy all-pass filter.
Conversely, we cannot get a long autocorrelation function
from a short signal.
A good example is the autocorrelation of a rectangle function,
which is a triangle.
The triangle appears to be twice as long,
but considering that the triangle tapers down,
it is reasonable to assert that the ![]() 's are the same.
Thus, we conclude that
's are the same.
Thus, we conclude that
![]() ,which is a simple idea.
,which is a simple idea.
![]()