




Next: Sample mean
Up: TIME-STATISTICAL RESOLUTION
Previous: Expectation and variance
A random variable x can be described by a
probability p(x) that
the amplitude x will be drawn.
In real life we almost never know the probability function,
but theoretically, if we do know it, we can compute the
mean value using
| 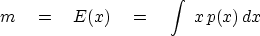 |
(16) |
``Statistical independence''
is a property of two or more random numbers.
It means the samples are drawn independently,
so they are unrelated to each other.
In terms of probability functions,
the independence of random variables x and y
is expressed by
| 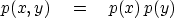 |
(17) |
From these, it is easy to show that
| 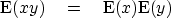 |
(18) |





Next: Sample mean
Up: TIME-STATISTICAL RESOLUTION
Previous: Expectation and variance
Stanford Exploration Project
10/21/1998