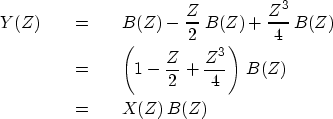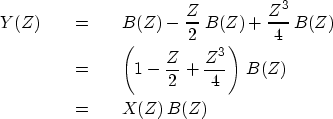Convolution with Z-transform

Now suppose there was an explosion at t = 0, a half-strength implosion at t = 1, and another, quarter-strength explosion at t = 3. This sequence of events determines a ``source'' time series, 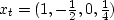$x_t = (1, -{1 \over 2}, 0, {1 \over 4})$.The Z-transform of the source is 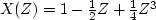$X(Z) = 1 - {1 \over 2}Z + {1 \over 4}Z^3$.The observed y_t for this sequence of explosions and implosions through the seismometer has a Z-transform Y(Z), given by

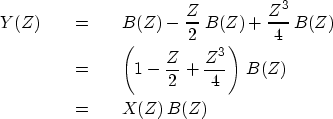$$\begin{eqnarray} Y(Z) &\eq & B(Z) - {Z \over 2}\, B(Z) + {Z^3 \over 4}\, B(Z) \n... ...2} + {Z^3 \over 4} \right)\, B(Z) \nonumber \ &\eq & X(Z)\, B(Z)\end{eqnarray}$$ (3)

The last equation shows polynomial multiplication as the underlying basis of time-invariant linear-system theory, namely that the output Y(Z) can be expressed as the input X(Z) times the impulse-response filter B(Z). When signal values are insignificant except in a ``small'' region on the time axis, the signals are called ``wavelets.''

There are many examples of linear systems. The one of most interest to us is wave propagation in the earth. A simpler example, around which a vast literature exists, is electronic filters. A cascade of filters is formed by taking the output of one filter and plugging it into the input of another. Suppose we have two linear filters characterized by B(Z) and C(Z). Then the question arises, illustrated in Figure 5, as to whether the two combined filters are equivalent.

 

commute Figure 5 Two equivalent filtering systems.

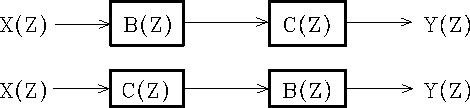The use of Z-transforms makes it obvious that these two systems are equivalent, since products of polynomials commute, i.e.,

$$\begin{eqnarray} Y_1(Z) &\eq & [X(Z) B(Z)]\, C(Z) \eq XBC \nonumber \ Y_2(Z) &\eq & [X(Z) C(Z)]\, B(Z) \eq XCB \eq XBC\end{eqnarray}$$ (4)