![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
We will not prove it here,
but this Gaussian-shaped signal
has a Fourier transform that also has a Gaussian shape,
.
We will not prove it here,
but this Gaussian-shaped signal
has a Fourier transform that also has a Gaussian shape,
The filter (1+Z)/2 is a running average of two adjacent time points.
Applying this filter N times yields the filter (1+Z)N/2N.
The coefficients of the filter (1+Z)N are generally known as
Pascal's triangle.
For large N the coefficients tend to a mathematical limit
known as a Gaussian function,
![]() , where
, where ![]() and t0 are constants that we will determine in chapter
and t0 are constants that we will determine in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
We will not prove it here,
but this Gaussian-shaped signal
has a Fourier transform that also has a Gaussian shape,
.
We will not prove it here,
but this Gaussian-shaped signal
has a Fourier transform that also has a Gaussian shape,
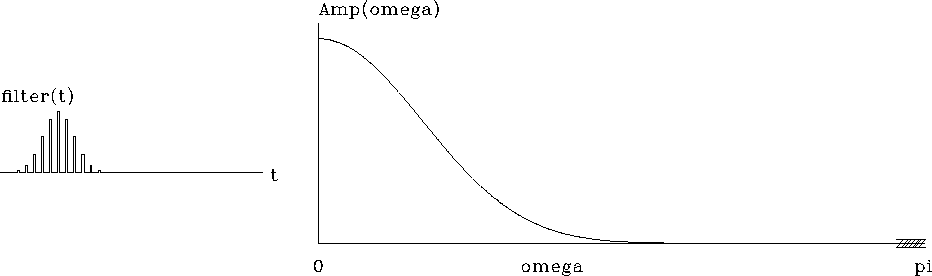
![]() .The Gaussian shape is often called a ``bell shape.''
Figure 8 shows an example for
.The Gaussian shape is often called a ``bell shape.''
Figure 8 shows an example for ![]() .Note that, except for the rounded ends,
the bell shape seems a good fit to a triangle function.
.Note that, except for the rounded ends,
the bell shape seems a good fit to a triangle function.
 |
Curiously, the filter (.75+.25Z)N also tends to the same Gaussian
but with a different t0.
A mathematical theorem
(discussed in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) says
that almost any polynomial raised to the N-th power yields a Gaussian.
) says
that almost any polynomial raised to the N-th power yields a Gaussian.
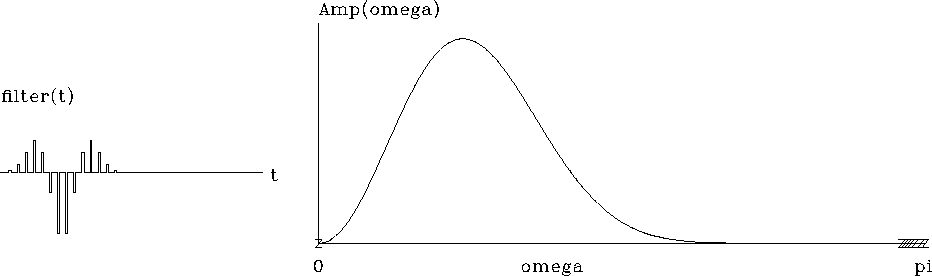
In seismology we generally fail to observe the zero frequency. Thus the idealized seismic pulse cannot be a Gaussian. An analytic waveform of longstanding popularity in seismology is the second derivative of a Gaussian, also known as a ``Ricker wavelet.''
Starting from the Gaussian and putting two more zeros at the origin with (1-Z)2=1-2Z+Z2 produces this old, favorite wavelet, shown in Figure 9.
 |