




Next: FOURIER AND Z-TRANSFORM
Up: FOURIER SUMS
Previous: Sampled time and Nyquist
In the previous section we superposed uniformly spaced frequencies.
Now we will superpose delayed impulses.
The frequency function of a delayed impulse at time delay t0
is 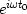 .Adding some pulses yields the ``Fourier sum'':
.Adding some pulses yields the ``Fourier sum'':
| 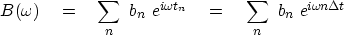 |
(19) |
The Fourier sum transforms the signal bt
to the frequency function 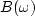 .Time will often be denoted by t, even though
its units are sample units instead of physical units.
Thus we often see bt in equations like (19) instead of bn,
resulting in an implied
.Time will often be denoted by t, even though
its units are sample units instead of physical units.
Thus we often see bt in equations like (19) instead of bn,
resulting in an implied 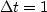 .
.





Next: FOURIER AND Z-TRANSFORM
Up: FOURIER SUMS
Previous: Sampled time and Nyquist
Stanford Exploration Project
10/21/1998