| NMO | ||
| Levin's NMO | ||
| DMO | ||
Hale [1983] found a Fourier representation of dip moveout. Refer to the defining equations in Table 1.
| NMO | ||
| Levin's NMO | ||
| DMO | ||
To use the dip-dependent equations in Table 7.1
it is necessary to know the earth dip ![]() .The dip can be measured from a zero-offset section.
On the zero-offset section in Fourier space,
the sine of the dip is
.The dip can be measured from a zero-offset section.
On the zero-offset section in Fourier space,
the sine of the dip is ![]() .To stress that this measurement applies only on the zero -offset section,
we shall always write
.To stress that this measurement applies only on the zero -offset section,
we shall always write ![]() .
.
| |
(9) |
In the absence of dip, NMO should convert any trace into
a replica of the zero-offset trace.
Likewise, in the presence of dip,
the combination of NMO and DMO
should convert any constant-offset section to a zero-offset section.
Pseudo-zero-offset sections manufactured in this way from
constant-offset sections will be denoted by p0 (t0 , h, y).
First take the midpoint coordinate y over to its Fourier dual ky.
Then take the Fourier transform over time
letting ![]() be Fourier dual to t0.
be Fourier dual to t0.
| |
(10) |
Change the variable of integration from t0 to tn.
| |
(11) |
| |
(12) |
Omitting the Jacobian (which does little), the over-all process may be envisioned with the program outline:
P(ky) =FT[P(y)]
Pn(tn) = NMO[P(t)]
for all ky { # three nested loops, interchangeable
for all h { # three nested loops, interchangeable
for all 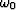 { # three nested loops, interchangeable
sum = 0
for all tn {
sum = sum +
{ # three nested loops, interchangeable
sum = 0
for all tn {
sum = sum + 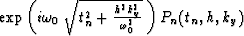 }
}
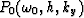 = sum
} } }
p0(t0, h, y) =FT2D
= sum
} } }
p0(t0, h, y) =FT2D![$[P_0(\omega_0, h, k_y)]$](img52.gif)
Notice that the exponential in the inner loop in the program does
not depend on velocity.
The velocity in the DMO equation in Table 7.1
disappears on substitution of ![]() from equation (9).
So dip moveout does not depend on velocity.
An example of processing with dip moveout is in
Figure 16.
from equation (9).
So dip moveout does not depend on velocity.
An example of processing with dip moveout is in
Figure 16.
 |
The procedure outlined above requires NMO before DMO. To reverse the order would be an approximation. This is unfortunate because we would prefer to do the costly, velocity-independent DMO step once, before the iterative, velocity-estimating NMO step.