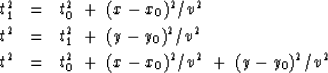
In an operations environment, 3-D is much harder to cope with than 2-D. Therefore, it may be expedient to suppose that 3-D migration can be achieved merely by application of 2-D migration twice, once in the x-direction and once in the y-direction. The previous section would lead you to believe that such an expedient process would result in a significant degradation of accuracy. In fact, the situation is much better than might be supposed. It has been shown by Jakubowicz and Levin [1983] that, wonder of wonders, for a constant-velocity medium, the expedient process is exact.
The explanation is this: migration consists of more than downward continuation. It also involves imaging, that is, the selection of data at t=0. In principle, downward continuation is first completed, for both the x and the y directions. After that, the imaging condition is applied. In the expedient process there are four steps: downward continuation in x, imaging, downward continuation in y, and finally a second imaging. Why it is that the expedient procedure gives the correct result seems something of a puzzle, but the validity of the result is easy to demonstrate.
First note that substitution of (7) into (8) gives (9) where
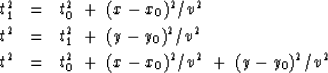 |
(7) | |
| (8) | ||
| (9) |
The Jakubowicz justification is somewhat more mathematical, but may be paraphrased as follows. First note that substitution of (10) into (11) gives (12) where
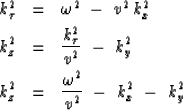 |
(10) | |
| (11) | ||
| (12) |
The validity of the Jakubowicz result
goes somewhat beyond its proof.
Our two-dimensional geophysicist may be
migrating other offsets besides zero offset.
(In chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) nonzero-offset data is migrated).
If a good job is done, all the reflected energy moves up
to the apex of the zero-offset hyperbola.
Then the cross-plane migration can handle it if it can handle zero offset.
So offset is not a problem.
But can a good job be done of bringing all the energy up to the apex
of the zero-offset hyperbola?
nonzero-offset data is migrated).
If a good job is done, all the reflected energy moves up
to the apex of the zero-offset hyperbola.
Then the cross-plane migration can handle it if it can handle zero offset.
So offset is not a problem.
But can a good job be done of bringing all the energy up to the apex
of the zero-offset hyperbola?
Difficulty arises when the velocity of the earth is depth-dependent, as it usually is. Then the Jakubowicz proof fails, and so does the expedient 3-D method. With a 2-D survey you have the problem that the sideswipe planes require a different migration velocity than the vertical plane. Rays propagating to the side take longer to reach the high-velocity media deep in the earth. So sideswipes usually require a lower migration velocity. If you really want to do three-dimensional migration with v(z), you should forget about separation and do it the hard way. Since we know how to transpose the hard way really isn't much harder.