A circumstance in which the degree of
noncommutativity of two differential operators
has a simple physical meaning and an obviously
significant geophysical application
is the so-called monochromatic 15![]() wave-extrapolation
equation in inhomogeneous media.
Adding and subtracting a constant term
to the unretarded
wave-extrapolation
equation in inhomogeneous media.
Adding and subtracting a constant term
to the unretarded ![]() equation gives us
equation gives us
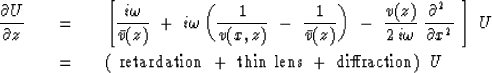 |
(4) | |
The problem is just that of focusing a slide projector. Adjusting the focus knob amounts to repositioning the thin-lens term in comparison to the free-space diffraction term. There is a small range of knob positions over which no one can notice any difference, and a larger range over which the people in the back row are not disturbed by misfocus. Much geophysical data processing amounts to downward extrapolation of data. The lateral variation of velocity occurring in the lens term is known only to a limited accuracy. The application could be to determine v(x) by the extrapolation procedure.
For long lateral spatial wavelengths the terms commute. Then diffraction may proceed in ignorance of the lateral variation in v. At shorter wavelengths the diffraction and lensing effects must be interspersed. So the real issue is not merely computational convenience but the interplay between data accuracy and the possible range for velocity in the underlying model.