




Next: Leapfrog equations
Up: INTRODUCTION TO STABILITY
Previous: Explicit 15 degree migration
Recall that the inflation-of-money equation
| 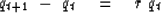 |
(73) |
is a simple explicit finite differencing
of the differential equation 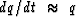 .And recall that a better approximation to the differential equation
is given by the Crank-Nicolson form
.And recall that a better approximation to the differential equation
is given by the Crank-Nicolson form
| 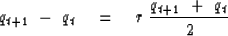 |
(74) |
that may be rearranged to
| 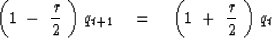 |
(75) |
or
| 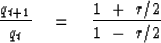 |
(76) |
The amplification factor (76) has magnitude less than unity for all
negative r values, even r equal to minus infinity.
Recall that the heat-flow equation corresponds to
| 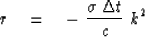 |
(77) |
where k is the spatial frequency.
Since (76) is good for all negative r, the heat-flow equation,
implicitly time-differenced, is
good for all spatial frequencies k.
The heat-flow equation
is stable whether or not the space axis
is discretized (then 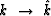 ) and
regardless of the sizes of
) and
regardless of the sizes of 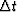 and
and 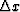 .Furthermore, the 15
.Furthermore, the 15 wave-extrapolation equation is also
unconditionally stable.
This follows from letting r in
(76) be purely imaginary: the
amplification factor (76) then takes the form of
some complex number 1 + r/2 divided by its complex conjugate.
Expressing the complex number in polar form, it becomes clear that such
a number has a magnitude exactly equal to unity.
Again there is unconditional stability.
wave-extrapolation equation is also
unconditionally stable.
This follows from letting r in
(76) be purely imaginary: the
amplification factor (76) then takes the form of
some complex number 1 + r/2 divided by its complex conjugate.
Expressing the complex number in polar form, it becomes clear that such
a number has a magnitude exactly equal to unity.
Again there is unconditional stability.
At this point it seems right to add a historical footnote.
When finite-difference migration was first introduced many objections
were raised on the basis that the theoretical assumptions
were unfamiliar.
Despite these objections finite-difference
migration quickly became popular.
I think the reason for its popularity
was that, compared to other methods of the time, it was
a gentle operation on the data.
More specifically,
since (76) is of exactly unit magnitude,
the output has the same 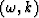 -spectrum as the input.
There may be a wider lesson to be learned from this experience:
any process acting on data should do as little to the data as possible.
-spectrum as the input.
There may be a wider lesson to be learned from this experience:
any process acting on data should do as little to the data as possible.





Next: Leapfrog equations
Up: INTRODUCTION TO STABILITY
Previous: Explicit 15 degree migration
Stanford Exploration Project
10/31/1997
![]() -spectrum as the input.
There may be a wider lesson to be learned from this experience:
any process acting on data should do as little to the data as possible.
-spectrum as the input.
There may be a wider lesson to be learned from this experience:
any process acting on data should do as little to the data as possible.