Definition of a recursive dip filter

Let P denote raw data and Q denote filtered data. When seismic data is quasimonochromatic, dip filtering can be achieved with spatial frequency filters. The table below shows filters with an adjustable cutoff parameter $\alpha$.

$$\omega\approx$$ 2|c|

Low Pass High Pass

$$Q \eq \displaystyle {\strut \alpha\over\alpha + k^2} \ P Q \eq \displaystyle {\strut k^2 \over\alpha + k^2} \ P$$

To apply these filters in the space domain it is necessary only to interpret k² as the tridiagonal matrix T with (-1,2,-1) on the main diagonal. Specifically, for the low-pass filter it is necessary to solve a tridiagonal set of simultaneous equations like  

$$(\,\alpha\,I\ +\ T\,) \ q\eq \alpha\ p$$ (21)

in which q and p are column vectors whose elements denote different places on the x-axis. Previously, this was done while solving the heat-flow equation. To make the filter space-variable, the parameter $\alpha$ can be taken to depend on x so that $\alpha\,I$ is replaced by an arbitrary diagonal matrix. It doesn't matter whether p and q are represented in the $\omega$-domain or the t-domain.

Turn your attention from narrow-band data to data with a somewhat broader spectrum and consider

$$\triangle\omega$$ 2|c|

Low Pass High Pass

$$Q \eq {\displaystyle {\strut \alpha} \over\displaystyle \alpha + {\strut k^2 \over -i\omega}} \ P Q \eq {\displaystyle {\strut k^2\over -i\omega} \over\displaystyle \alpha + {\strut k^2\over -i\omega}} \ P$$

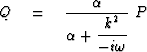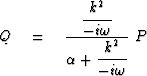Naturally these filters can be applied to data of any bandwidth. However the filters are appropriately termed ``dip filters'' only over a modest bandwidth.

To understand these filters look in the $( \omega , k)$-plane at contours of constant $k^2 / \omega ,$ i.e. $\omega \approx k^2$.Such contours, examples of which are shown in Figure 3, are curves of constant attenuation and constant phase shift.

 

dipfil Figure 3 Constant-attenuation contours of dip filters. Over the seismic frequency band these parabolas may be satisfactory approximations to the dashed straight line. Pass/reject zones are indicated for the low-pass filter. (Hale)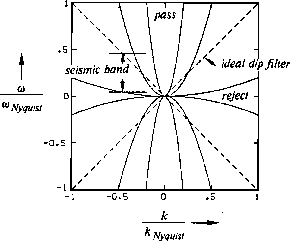

An interesting feature of these dip filters is that the low-pass and the high-pass filters constitute a pair of filters which sum to unity. So nothing is lost if a dataset is partitioned by them in two. The high-passed part could be added to the low-passed part to recover the original dataset. Alternately, once the low-pass output is computed, it is much easier to compute the high-pass output, because it is just the input minus the low-pass. The low-pass filter has no phase shift in the pass zone, but there is time differentiation in the attenuation zone. This is apparent from the defining equation. The high-pass filter has no phase shift in the flat pass zone, but there is time integration in the attenuating zone.