Slant stack and Fourier transform

Let u(x,t) be a wavefield. The slant stack $\bar u (p, \tau )$ of the wavefield is defined mathematically by  

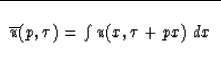$$\begin{tabular} {\vert c\vert} \hline \\ $\overline{u}(p, \tau) = \int u(x, \tau + px)\ dx$ \\ \\ \hline\end{tabular}$$ (14)

The integral across x in (14) is done at constant $\tau$, which is a slanting line in the (x,t)-plane.

Slant stack is readily expressed in Fourier space. The definition of the two-dimensional Fourier transformation of the wavefield u(x,t) is  

$$U(k, \omega ) \eq \int \int \ e^{{i} \omega t \,-\, i k x} \ u(x,t)\ dx\ dt$$ (15)

Recall the definition of Snell's parameter in Fourier space $p=k/ \omega$ and use it to eliminate k from the 2-D Fourier transform (15).  

$$U( \omega p , \omega ) \eq \int \int \ e^{{i} \omega (t\,-\,px) } \ u(x,t)\ dx\ dt$$ (16)

Change the integration variable from t to $\tau = t-px$. 

$$U( \omega p , \omega ) \eq \int \ e^{{i}\omega\tau} \ [\ \int \ u(x, \tau \,+\,px )\ dx\ ]\ d \tau$$ (17)

Insert the definition (14) into (17).  

$$U( \omega p , \omega ) \eq \int \ e^{{i} \omega \tau } \ \, {\bar u} ( p, \tau ) \ d \tau$$ (18)

Think of $U( \omega p, \omega )$ as a one-dimensional function of $\omega$that is extracted from the $(k, \omega )$-plane along the line $k = \omega p$.

The inverse Fourier transform of (18) is  

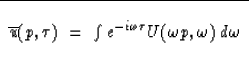$$\begin{tabular} {\vert c\vert} \hline \\ $\overline{u}(p, \... ...U(\omega p, \omega)\ d\omega$\space \\ \\ \hline\end{tabular}$$ (19)

The result (19) states that a slant stack can be created by Fourier-domain operations. First you transform u(x,t) to $U( k , \omega )$.Then extract $U( \omega p, \omega )$ from $U( k , \omega )$.Finally, inverse transform from $\omega$ to $\tau$ and repeat the process for all interesting values of p.

Getting $U( \omega p, \omega )$ from $U( k , \omega )$ seems easy, but this turns out to be the hard part. The line $k = \omega p$ will not pass nicely through all the mesh points (unless $p=\Delta t / \Delta x$) so some interpolation must be done. As we have seen from the computational artifacts of Stolt migration, Fourier-domain interpolation should not be done casually.

Both (14) and (19) are used in practice. In (14) you have better control of truncation and aliasing. For large datasets, (19) is much faster.