




Next: WAVEMOVIE PROGRAM
Up: FINITE DIFFERENCING
Previous: The xxz derivative
So far we have had no trouble obtaining cheap, safe, and accurate
difference methods for solving
partial-differential equations
(PDEs).
The implicit method has met all needs.
But in space dimensions higher than one, the implicit method becomes
prohibitively costly.
For the common example of problems in which
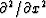 becomes generalized to
becomes generalized to
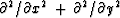 ,we will learn the reason why.
The simplest case is the heat-flow equation for which the Crank-Nicolson
method gave us (37).
Introducing the abbreviation
,we will learn the reason why.
The simplest case is the heat-flow equation for which the Crank-Nicolson
method gave us (37).
Introducing the abbreviation 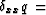 qx+1 -2qx + qx-1,
equation (37) becomes
qx+1 -2qx + qx-1,
equation (37) becomes
| 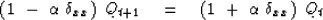 |
(48) |
The nested expression on the left represents a tridiagonal matrix.
The critical stage is in solving the tridiagonal simultaneous
equations for the vector of unknowns 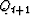 .Fortunately there is a special algorithm for this solution,
and the cost increases only linearly with the size of the matrix.
Now turn from the one-dimensional physical space of x to
two-dimensional (x,y)-space.
Letting
.Fortunately there is a special algorithm for this solution,
and the cost increases only linearly with the size of the matrix.
Now turn from the one-dimensional physical space of x to
two-dimensional (x,y)-space.
Letting  denote the numerical constant in (48), the
equation for stepping forward in time is
denote the numerical constant in (48), the
equation for stepping forward in time is
| ![\begin{displaymath}[ \, 1\ -\ \alpha\ ( \delta_{{xx}} \ +\ \delta_{{yy}} ) \ ]
\...
...
[ 1\ +\ \alpha ( \delta_{{xx}} \ +\ \delta_{{yy}} ) \ ] \
Q_t\end{displaymath}](img127.gif) |
(49) |
The unknowns Qt+1 are a
two-dimensional function of x and y that
can be denoted by a matrix.
Next we will interpret the bracketed expression on the left side.
It turns out to be a four-dimensional matrix!
To clarify the meaning of this matrix, a mapping from two
dimensions to one will be illustrated.
Take the temperature Q to be defined on a 4 4 mesh.
A natural way of numbering the points on the mesh is
4 mesh.
A natural way of numbering the points on the mesh is
|  |
(50) |
For algebraic purposes these sixteen numbers can be mapped into a vector.
There are many ways to do this.
A simple way would be to associate the locations in (50)
with vector components by the column arrangement
|  |
(51) |
The second difference operator has the following star in the (x,y)-plane:
|  |
(52) |
Lay this star down in
the (x,y)-plane (51) and move it around.
Unfortunately, with just sixteen points, much of what you see is dominated
by edges and corners.
Try every position of the star that allows the center -4
to overlay one of the sixteen points.
Never mind the 1's going off the sides.
Start with the -4 in (52)
over the 1 in the upper left corner of (51).
Observe 1's on the 2 and the 5.
Copy the 1's into the top row of Table 4.8 into
the second and fifth columns.
Then put the -4 in (52) over the 2 in (51).
Observe 1's on the 1, 3, and 6.
Copy the 1's into the next row of Table 4.8.
Then put the -4 over the 3.
Observe 1's on the 2, 4, and 7.
Continue likewise. The
16 16 square matrix that results is shown in Table 4.8.
16 square matrix that results is shown in Table 4.8.
Now that Table 4.8 has been constructed
we can return to the interpretation
of equation (49).
The matrix of unknowns Qt+1 has been mapped into a sixteen-point
column vector, and the bracketed expression
multiplying Qt+1 can be mapped into a 16 16 matrix.
Clearly,
the matrix contains zeroes everywhere that Table 4.8 contains dots.
It seems fortunate that the table contains many zeroes,
and we are led to hope
for a rapid solution method for the simultaneous equations.
The bad news is that no good method has ever been found.
The best methods seem to require effort
proportional to N3, where in this
case N=4.
Based on our experience in one dimension,
those of us who worked on this
problem hoped for a method
proportional to N2, which is the cost of an explicit
method--essentially
the cost of computing the right side of (41).
Even all the features of implicit methods do not justify
an additional cost of a factor
of N.
The next best thing is the splitting method.
16 matrix.
Clearly,
the matrix contains zeroes everywhere that Table 4.8 contains dots.
It seems fortunate that the table contains many zeroes,
and we are led to hope
for a rapid solution method for the simultaneous equations.
The bad news is that no good method has ever been found.
The best methods seem to require effort
proportional to N3, where in this
case N=4.
Based on our experience in one dimension,
those of us who worked on this
problem hoped for a method
proportional to N2, which is the cost of an explicit
method--essentially
the cost of computing the right side of (41).
Even all the features of implicit methods do not justify
an additional cost of a factor
of N.
The next best thing is the splitting method.
Table 8:
The two-dimensional matrix of coefficients for the Laplacian operator.
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -4 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
-4 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-4 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
-4 |
1 |
|
|
1 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
1 |
|
|
1 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
1 |
|
|
1 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
|
|
|
1 |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
-4 |
1 |
|
|
1 |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
1 |
|
|
1 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
1 |
|
|
1 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
|
|
|
1 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
-4 |
1 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
1 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
1 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
-4 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EXERCISES:
-
Interpret the inflation-of-money equation when the interest rate
is the imaginary number i/10.
-
Write the 45
 diffraction equation
in (x,z)-space for fixed
diffraction equation
in (x,z)-space for fixed 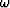 in the form of (36).
in the form of (36).





Next: WAVEMOVIE PROGRAM
Up: FINITE DIFFERENCING
Previous: The xxz derivative
Stanford Exploration Project
10/31/1997
![]() becomes generalized to
becomes generalized to
![]() ,we will learn the reason why.
The simplest case is the heat-flow equation for which the Crank-Nicolson
method gave us (37).
Introducing the abbreviation
,we will learn the reason why.
The simplest case is the heat-flow equation for which the Crank-Nicolson
method gave us (37).
Introducing the abbreviation ![]() qx+1 -2qx + qx-1,
equation (37) becomes
qx+1 -2qx + qx-1,
equation (37) becomes
![]() 4 mesh.
A natural way of numbering the points on the mesh is
4 mesh.
A natural way of numbering the points on the mesh is



![]() 16 square matrix that results is shown in Table 4.8.
16 square matrix that results is shown in Table 4.8.
![]() 16 matrix.
Clearly,
the matrix contains zeroes everywhere that Table 4.8 contains dots.
It seems fortunate that the table contains many zeroes,
and we are led to hope
for a rapid solution method for the simultaneous equations.
The bad news is that no good method has ever been found.
The best methods seem to require effort
proportional to N3, where in this
case N=4.
Based on our experience in one dimension,
those of us who worked on this
problem hoped for a method
proportional to N2, which is the cost of an explicit
method--essentially
the cost of computing the right side of (41).
Even all the features of implicit methods do not justify
an additional cost of a factor
of N.
The next best thing is the splitting method.
16 matrix.
Clearly,
the matrix contains zeroes everywhere that Table 4.8 contains dots.
It seems fortunate that the table contains many zeroes,
and we are led to hope
for a rapid solution method for the simultaneous equations.
The bad news is that no good method has ever been found.
The best methods seem to require effort
proportional to N3, where in this
case N=4.
Based on our experience in one dimension,
those of us who worked on this
problem hoped for a method
proportional to N2, which is the cost of an explicit
method--essentially
the cost of computing the right side of (41).
Even all the features of implicit methods do not justify
an additional cost of a factor
of N.
The next best thing is the splitting method.