![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .3 and
.3 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4 is arrived at by splitting.
That is, you march forward a small
.4 is arrived at by splitting.
That is, you march forward a small
The customary numerical solution to the x-domain forms of the equations
in Tables ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .3 and
.3 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4 is arrived at by splitting.
That is, you march forward a small
.4 is arrived at by splitting.
That is, you march forward a small ![]() -step alternately
with the two extrapolators
-step alternately
with the two extrapolators
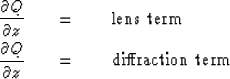 |
(18) | |
| (19) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The first equation, called the
lens equation,
is solved analytically:
.
The first equation, called the
lens equation,
is solved analytically:
| |
(20) |
Migrations that include the lens equation are called depth migrations. The term is often omitted, giving a time migration.
Observe that the diffraction parts of Tables ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .3 and
.3 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .4 are the same.
Let us use them and equation (19) to
define a table of diffraction equations.
Substitute
.4 are the same.
Let us use them and equation (19) to
define a table of diffraction equations.
Substitute ![]() for i kx and
clear
for i kx and
clear ![]() from the denominators to
get Table
from the denominators to
get Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .5.
.5.