




Next: The DSR equation in
Up: SURVEY SINKING WITH THE
Previous: The survey-sinking concept
An equation was derived for paraxial waves.
The assumption of a
single
plane wave means that the arrival time
of the wave is given by a single-valued t(x,z).
On a plane of constant z, such as the earth's surface,
Snell's parameter p is measurable.
It is
| 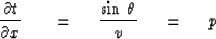 |
(24) |
In a borehole there is the constraint that measurements
must be made
at a constant x, where the relevant measurement from an
upcoming
wave would be
| 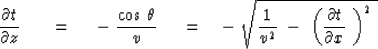 |
(25) |
Recall the time-shifting partial-differential equation and its
solution U as some arbitrary functional form f:
| 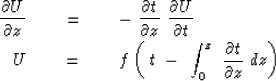 |
(26) |
| (27) |
The partial derivatives
in equation (26) are taken to be at constant x,
just as is equation (25).
After inserting (25) into (26) we have
| 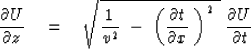 |
(28) |
Fourier transforming the wavefield over (x,t), we
replace 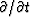 by
by 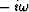 .Likewise, for the traveling wave
of the Fourier kernel
.Likewise, for the traveling wave
of the Fourier kernel 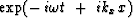 ,constant phase means that
,constant phase means that 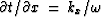 .With this, (28) becomes
.With this, (28) becomes
| 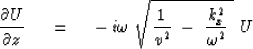 |
(29) |
The solutions to (29) agree with those to the scalar wave equation
unless v is a function of z, in which case
the scalar wave equation has both upcoming and downgoing solutions,
whereas (29) has only upcoming solutions.
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) taught us how to go into the lateral space
domain by replacing i kx by
taught us how to go into the lateral space
domain by replacing i kx by 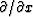 .The resulting equation is useful for superpositions of many local plane waves
and for lateral velocity variations v(x).
.The resulting equation is useful for superpositions of many local plane waves
and for lateral velocity variations v(x).





Next: The DSR equation in
Up: SURVEY SINKING WITH THE
Previous: The survey-sinking concept
Stanford Exploration Project
10/31/1997
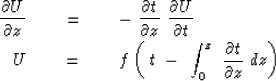
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) taught us how to go into the lateral space
domain by replacing i kx by
taught us how to go into the lateral space
domain by replacing i kx by