Cheops' pyramid

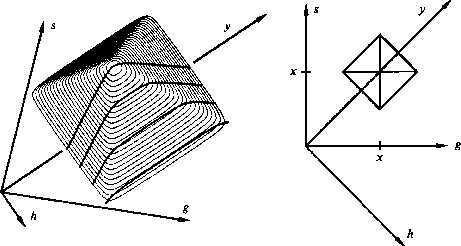
Because of the importance of the point-scatterer model, we will go to considerable lengths to visualize the functional dependence among t, z, x, s, and g in equation (5). This picture is more difficult--by one dimension--than is the conic section of the exploding-reflector geometry.

To begin with, suppose that the first square root in (5) is constant because everything in it is held constant. This leaves the familiar hyperbola in (g,t)-space, except that a constant has been added to the time. Suppose instead that the other square root is constant. This likewise leaves a hyperbola in (s,t)-space. In (s,g)-space, travel time is a function of s plus a function of g. I think of this as one coat hanger, which is parallel to the s-axis, being hung from another coat hanger, which is parallel to the g-axis.

A view of the travel-time pyramid on the (s,g)-plane or the (y,h)-plane is shown in Figure 18a.

 

cheop
Figure 18 Left is a picture of the travel-time pyramid of equation for fixed x and z. The darkened lines are constant-offset sections. Right is a cross section through the pyramid for large t (or small z). (Ottolini)

Notice that a cut through the pyramid at large t is a square, the corners of which have been smoothed. At very large t, a constant value of t is the square contoured in (s,g)-space, as in Figure 18b. Algebraically, the squareness becomes evident for a point reflector near the surface, say, $z \to 0$.Then (5) becomes  

$$v\,t\ \eq \ \vert s \ -\ x \vert\ \ +\ \ \vert g \ -\ x \vert$$ (6)

The center of the square is located at (s,g) = (x,x). Taking travel time t to increase downward from the horizontal plane of (s,g)-space, the square contour is like a horizontal slice through the Egyptian pyramid of Cheops. To walk around the pyramid at a constant altitude is to walk around a square. Alternately, the altitude change of a traverse over g at constant s is simply a constant plus an absolute-value function, as is a traverse of s at constant g.

More interesting and less obvious are the curves on common-midpoint gathers and constant-offset sections. Recall the definition that the midpoint between the shot and geophone is y. Also recall that h is half the horizontal offset from the shot to the geophone.

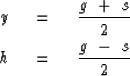$$\begin{eqnarray} y\ \ &=&\ \ {g \ +\ s \over 2 } \\ h\ \ &=&\ \ {g \ -\ s \over 2 }\end{eqnarray}$$ (7) (8)

A traverse of y at constant h is shown in Figure 18. At the highest elevation on the traverse, you are walking along a flat horizontal step like the flat-topped hyperboloids of Figure 16. Some erosion to smooth the top and edges of the pyramid gives a model for nonzero reflector depth.

For rays that are near the vertical, the travel-time curves are far from the hyperbola asymptotes. Then the square roots in (5) may be expanded in Taylor series, giving a parabola of revolution. This describes the eroded peak of the pyramid.