 |
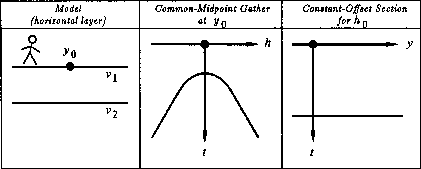
Figure 12 Simplest earth model.
The simplest environment for reflection data is a single horizontal reflection interface, which is shown in Figure 12.
 |
As expected, the zero-offset section mimics the earth model. The common-midpoint gather is a hyperbola whose asymptotes are straight lines with slopes of the inverse of the velocity v1. The most basic data processing is called common-depth-point stack or CDP stack. In it, all the traces on the common-midpoint (CMP) gather are time shifted into alignment and then added together. The result mimics a zero-offset trace. The collection of all such traces is called the CDP-stacked section. In practice the CDP-stacked section is often interpreted and migrated as though it were a zero-offset section. In this chapter we will learn to avoid this popular, oversimplified assumption.
The next simplest environment is to have a planar reflector that is oriented vertically rather than horizontally. This is not typical, but is included here because the effect of earth dip is more comprehensible in an extreme case. Now the wave propagation is along the air-earth interface. To avoid confusion the reflector may be inclined at a slight angle from the vertical, as in Figure 13.
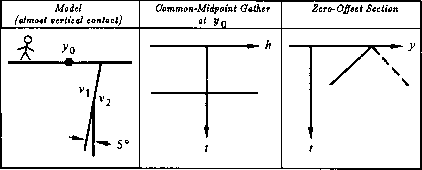 |
Figure 13 shows that the travel time does not change as the offset changes. It may seem paradoxical that the travel time does not increase as the shot and geophone get further apart. The key to the paradox is that midpoint is held constant, not shotpoint. As offset increases, the shot gets further from the reflector while the geophone gets closer. Time lost on one path is gained on the other.
A planar reflector may have any dip between horizontal and vertical. Then the common-midpoint gather lies between the common-midpoint gather of Figure 12 and that of Figure 13. The zero-offset section in Figure 13 is a straight line, which turns out to be the asymptote of a family of hyperbolas. The slope of the asymptote is the inverse of the velocity v1.