Hard sea floor example

Figure 1 shows textbook-quality multiple reflections from the sea floor. Hyperbolas $v^2 \, t^2 \,-\,x^2 \,=\, z_j^2$ appear at uniform intervals $z_j \,=\, j\,\Delta Z,$ j=0,1,2, .... The data is unprocessed other than by multiplication by a spherical divergence correction t. Air is slower and lighter than water while sea-floor sediment is almost always faster and denser. This means that successive multiple reflections almost always have alternating polarity. The polarity of a seismic arrival is usually ambiguous, but here the waveform is distinctive and it clearly alternates in polarity from bounce to bounce. The ratio of amplitudes of successive multiple reflections is the reflection coefficient. In Figure 1, the reflection coefficient seems to be about $-\,0.7$.

 

multiple
Figure 1 Marine profile of multiple reflections from Norway. At the right, the near trace is expanded. (GECO)

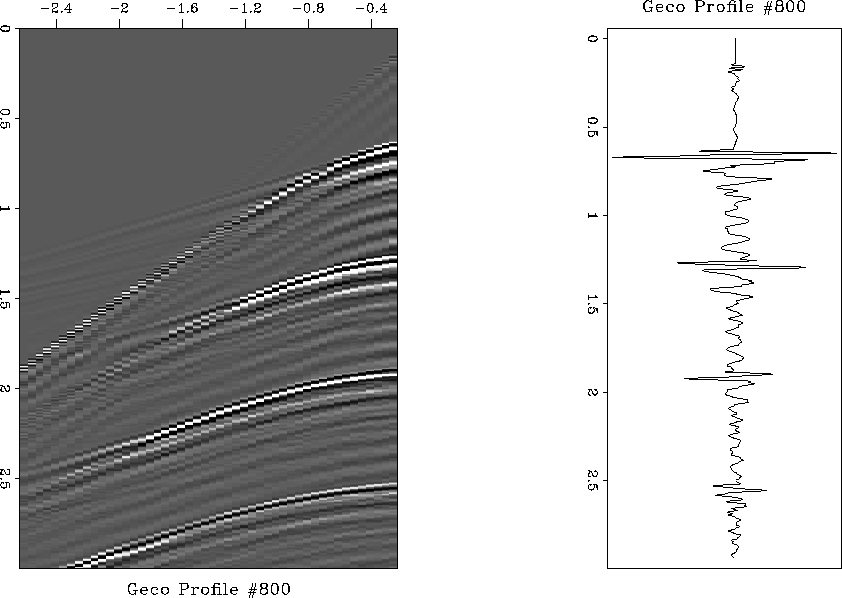Multiply reflected head waves are also apparent, as are alternating polarities on them. Since the head-wave multiple reflections occur at critical angle, they should have a -1.0 reflection coefficient. We see them actually increasing from bounce to bounce. The reason for the increase is that the spherical-divergence correction is based on three-dimensional propagation, while the head waves are really spreading out in two dimensions.

Multiple reflections are fun for wave theorists, but they are a serious impediment to geophysicists who would like to see the information-bearing primary reflections that they mask.