




Next: Migration with moveout correction
Up: PROFILE IMAGING
Previous: PROFILE IMAGING
The U/D imaging concept says that
reflectors exist in the earth at places where the onset of the downgoing wave
is time-coincident with an upcoming wave.
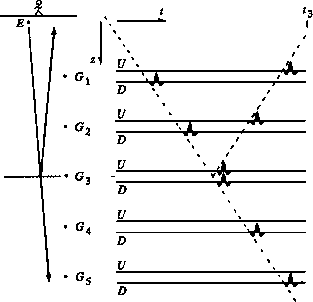
Figure 17 illustrates the concept.
udimage
Figure 17
Upcoming and downgoing waves observed with buried receivers.
A disturbance leaves the surface at t = 0 and is observed passing
the buried receivers G1...G5 at progressively later times.
At the depth of a reflector, z3,
the G3 receiver records
both the upcoming and downgoing waves in time coincidence.
Shallower receivers also record both waves.
Deeper receivers record only D.
The fundamental principle of reflector mapping
states that reflectors exist
where U and D are time-coincident.
(Riley)
|
|  |

It is easy to confuse the
survey-sinking
concept with the U/D concept because of the similarity
of the phrases used to describe them: ``downward continue the shots''
sounds like ``downward continue the downgoing wave.''
The first concept refers to computations involving only an
upcoming wavefield U(s,g,z,t).
The second concept refers to computations
involving both upcoming U(x,z,t) and downgoing D(x,z,t) waves.
No particular source location enters the U/D concept;
the source could be a downgoing plane wave.
In profile migration methods,
the downgoing wave is usually handled theoretically,
typically as an impulse
whose travel time is known analytically or by ray tracing.
But this is not important: the downgoing wave
could be handled the same way as the upcoming wave,
by the Fourier or finite-difference methods
described in previous chapters.
The upcoming wave could be expressed in Cartesian coordinates,
or in the moveout coordinate system to be described below.
The time coincidence
of the downgoing and upcoming waves
can be quantified in several ways.
The most straightforward seems to be to look at the
zero lag of the cross-correlation of the two waves.
The image is created by displaying the zero-lagged cross-correlation
everywhere in (x,z)-space.
The time coincidence of the upcoming wave and the earliest
arrival of a downgoing wave gives evidence of the existence
of a reflector, but in principle, more can be learned from
the two waves.
The amplitude ratio of the upcoming to the downgoing wave
gives the reflection coefficient.
In the Fourier domain,
the product 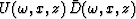 represents
the zero lag of the cross-correlation.
The reflection coefficient ratio is given
by
represents
the zero lag of the cross-correlation.
The reflection coefficient ratio is given
by 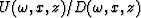 .This ratio has many difficulties.
Not only may the denominator be zero,
but it may have zeroes in the wrong part of the complex plane.
This happens when the downgoing wave is causal but not
minimum phase.
The phase of the complex conjugate of a complex number
equals the phase of the inverse of the number.
Thus the ratio U/D and the product
.This ratio has many difficulties.
Not only may the denominator be zero,
but it may have zeroes in the wrong part of the complex plane.
This happens when the downgoing wave is causal but not
minimum phase.
The phase of the complex conjugate of a complex number
equals the phase of the inverse of the number.
Thus the ratio U/D and the product 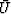 both have the same phase.
It seems you can invent other functional forms that compromise
the theoretical appeal of U/D with the stability of
both have the same phase.
It seems you can invent other functional forms that compromise
the theoretical appeal of U/D with the stability of 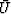 .
.
Don C. Riley [1974] proposed another form of the U/D principle,
namely,
that the upcoming waves must vanish
for all time before the first arrival of the downgoing wave.
Riley's form found use in wave-equation dereverberation.





Next: Migration with moveout correction
Up: PROFILE IMAGING
Previous: PROFILE IMAGING
Stanford Exploration Project
10/31/1997
