




Next: Lightning phase shift migration
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: Retarded Muir recurrence
If you are using finite differences on depth,
or travel-time depth,
then we have the relation (46):
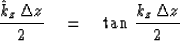
which can be used in 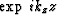 .Since dissipation may be present,
the quantities above may be complex.
Let Nz be the number of depth layers,
generally equal or less than Nt.
Adapting (49) to (59) gives
.Since dissipation may be present,
the quantities above may be complex.
Let Nz be the number of depth layers,
generally equal or less than Nt.
Adapting (49) to (59) gives
| 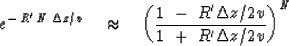 |
(60) |





Next: Lightning phase shift migration
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: Retarded Muir recurrence
Stanford Exploration Project
10/31/1997
![]()