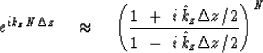Next: ACCURACY THE CONTRACTOR'S VIEW
Up: FREQUENCY DISPERSION IN WAVE-MIGRATION
Previous: The 1/6 trick
You might be inclined to think a second derivative is a
second derivative and that there is no mathematical reason to do
time derivatives differently than space derivatives.
This is not the case.
A hint of disparity
between t and x derivatives comes from boundary conditions.
With time derivatives
(and often with the depth z derivative)
we must consider causality--which
means the future is determined solely from the present and past.
Appropriate boundary conditions on the time axis
are initial conditions--the function (and perhaps some derivatives)
is specified at
one
point, the initial point in time.
For depth z that special point is the earth's surface at z=0.
But lateral space derivatives are different:
they require boundary conditions at two widely separated points,
usually at the left and right sides of the volume.
The differential equation
| 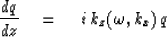 |
(42) |
is associated with the very definition of kz .
The analogous difference equation will define 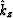 :
:
| 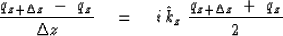 |
(43) |
Inserting the
solution of (42)
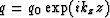 into (43) gives
us the relation between the desired kz and the actual
into (43) gives
us the relation between the desired kz and the actual 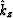 .
.
| 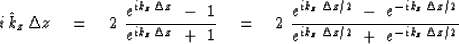 |
(44) |
This equation is known as the bilinear transform.
| 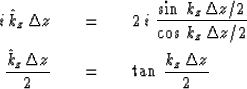 |
(45) |
| (46) |
Equation (46) gives the accuracy of
first derivatives obtained using the Crank-Nicolson method.
Recall the migration differencing schemes in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
We did the time differencing in the same way that we did the depth
differencing.
So the same accuracy limitation must apply, namely,
.
We did the time differencing in the same way that we did the depth
differencing.
So the same accuracy limitation must apply, namely,
| 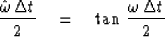 |
(47) |
Series expansion shows
that 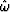 goes to
goes to 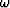 as
as 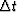 goes to zero.
Relative errors in
goes to zero.
Relative errors in 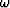 at (4, 10, and 20) points per wavelength
are (30%, 3%, and 1%).
These errors are quite large,
calling for either a choice
of small
at (4, 10, and 20) points per wavelength
are (30%, 3%, and 1%).
These errors are quite large,
calling for either a choice
of small 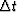 or a more accurate method than (46).
or a more accurate method than (46).
The bad news is that there does not seem to exist a representation of causal
differentiation that is any more accurate than the Crank-Nicolson
representation.
There is nothing like the 1/6 trick.
Thus the sample intervals of 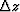 and
and 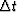 must be reduced
considerably from the Nyquist criterion.
The practical picture may not be as bleak as the one I am painting.
Many people are pleased with both the speed and accuracy of time-domain
migrations at
must be reduced
considerably from the Nyquist criterion.
The practical picture may not be as bleak as the one I am painting.
Many people are pleased with both the speed and accuracy of time-domain
migrations at 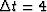 milliseconds.
milliseconds.
Stolt's classic paper [1978]
besides introducing the fast Fourier transform migration method,
points out that more accuracy can be achieved
when the requirement of causality is dropped.
Stolt shows how dropping causality at the known depth level
while retaining it at the next level allows stable finite differencing.
With the depth z-axis we are stuck with causal derivatives,
although Fourier methods could be used for discrete layers.
The depth axis is not so troublesome as
the x- and t-axes, however, because it affects computer time only,
not data storage.
Finite difference solutions don't just approximate the frequency--what
they really do is to approximate 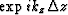 .Solve (43) for the unknown.
.Solve (43) for the unknown.
| 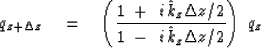 |
(48) |
So for Nz layers in depth 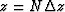 we
have the approximation
we
have the approximation
| 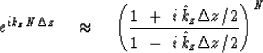 |
(49) |
which will be of later use
for Fourier domain simulations of finite difference programs.
Such simulations
enable us to compare the accuracy
of various migration methods.





Next: ACCURACY THE CONTRACTOR'S VIEW
Up: FREQUENCY DISPERSION IN WAVE-MIGRATION
Previous: The 1/6 trick
Stanford Exploration Project
10/31/1997
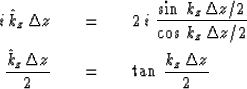
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
We did the time differencing in the same way that we did the depth
differencing.
So the same accuracy limitation must apply, namely,
.
We did the time differencing in the same way that we did the depth
differencing.
So the same accuracy limitation must apply, namely,
![]() and
and ![]() must be reduced
considerably from the Nyquist criterion.
The practical picture may not be as bleak as the one I am painting.
Many people are pleased with both the speed and accuracy of time-domain
migrations at
must be reduced
considerably from the Nyquist criterion.
The practical picture may not be as bleak as the one I am painting.
Many people are pleased with both the speed and accuracy of time-domain
migrations at ![]() milliseconds.
milliseconds.
![]() .Solve (43) for the unknown.
.Solve (43) for the unknown.