




Next: ANISOTROPY DISPERSION IN MIGRATION
Up: COSMETIC ASPECT OF WAVE
Previous: Exponential scaling
The 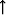 operator has been defined as
the substitution
operator has been defined as
the substitution 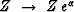 .The main property of this operator is that
if C=AB, then C=(A)(B).
This property would be shared by
any algebraic substitution for Z,
not just the one for exponential gain.
Another simple substitution can be used to achieve time-axis
stretching or compression.
For example, replacing Z by Z2 stretches the time axis by two.
Yet another substitution, which has a deeper meaning than
either of the previous two, is the substitution
of the constant Q dissipation operator
.The main property of this operator is that
if C=AB, then C=(A)(B).
This property would be shared by
any algebraic substitution for Z,
not just the one for exponential gain.
Another simple substitution can be used to achieve time-axis
stretching or compression.
For example, replacing Z by Z2 stretches the time axis by two.
Yet another substitution, which has a deeper meaning than
either of the previous two, is the substitution
of the constant Q dissipation operator 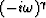 .In summary:
.In summary:
| 2|c| |
|
| 2|c|Substitutions for Z-Transform
Variable Z |
|
|---|
| 2|c|[all preserve C(Z)=A(Z)B(Z)] |
|
| 2|c| |
|
| |
|
| Exponential growth |
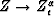 |
| |
(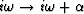 ) ) |
| |
|
| |
|
Time expansion (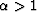 ) ) |
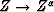 |
| |
|
| |
|
| (Inverse) Constant Q dissipation |
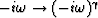 |
| |
|
EXERCISES:
-
Use a table of integrals to show that a seismic source
with spectrum
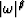 implies a divergence
correction
implies a divergence
correction 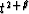 .
. -
Assuming that t2 is a suitable divergence correction
for field profiles,
what divergence correction should be applied to CDP stacks?
-
How is the t2 correction altered for water of travel
time depth t0?
Assume the Q of water is infinite.
-
Consider a source spectrum
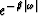 .How is the t2 correction altered?
.How is the t2 correction altered?
-
The spectrum in Figure 3 shows high frequencies smoother
than low frequencies.
Explain.
-
Propose some criteria that can be used in the selection of
the cutoff parameters
 and
and 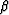 for the filter (8).
for the filter (8).





Next: ANISOTROPY DISPERSION IN MIGRATION
Up: COSMETIC ASPECT OF WAVE
Previous: Exponential scaling
Stanford Exploration Project
10/31/1997
![]() operator has been defined as
the substitution
operator has been defined as
the substitution ![]() .The main property of this operator is that
if C=AB, then C=(A)(B).
This property would be shared by
any algebraic substitution for Z,
not just the one for exponential gain.
Another simple substitution can be used to achieve time-axis
stretching or compression.
For example, replacing Z by Z2 stretches the time axis by two.
Yet another substitution, which has a deeper meaning than
either of the previous two, is the substitution
of the constant Q dissipation operator
.The main property of this operator is that
if C=AB, then C=(A)(B).
This property would be shared by
any algebraic substitution for Z,
not just the one for exponential gain.
Another simple substitution can be used to achieve time-axis
stretching or compression.
For example, replacing Z by Z2 stretches the time axis by two.
Yet another substitution, which has a deeper meaning than
either of the previous two, is the substitution
of the constant Q dissipation operator ![]() .In summary:
.In summary: