




Next: Application to 45 degree
Up: THE BULLETPROOFING OF MUIR
Previous: Stability of the differential
The stability of the difference equation can be shown in a similar way, but
with some extra clutter.
First observe the identity
| ![\begin{displaymath}
( a^ { {\rm *} \, } a\ -\ \b^ {{\rm *}\,} \b ) \ \ \ \equiv
...
...}
( a\ -\ \b ) \ +\ ( a\ -\ \b )^ { {\rm *} \, } ( a\ +\ \b )]\end{displaymath}](img218.gif) |
(84) |
Letting 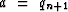 and
and 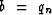 ,equation (84) becomes
,equation (84) becomes
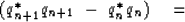
| ![\begin{displaymath}
\ \ \eq
{1 \over 2}\ [(q_{n+1} \ +\ q_n )^{{\rm *}\,} ( q_{...
... +\
( q_{n+1} \ -\ q_n )^ { {\rm *} \, } ( q_{n+1} \ +\ q_n )]\end{displaymath}](img222.gif) |
(85) |
Now, replace the 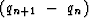 terms by
equation (81):
terms by
equation (81):
![\begin{displaymath}
\eq -\ {\Delta z \over 4}\ [
\ ( q_{n+1}+ q_n )^{{\rm *}\,}
...
...n )+
(q_{n+1}+q_n )^{{\rm *}\,}
R^{{\rm *}}
\,(q_{n+1}+q_n )]\end{displaymath}](img224.gif)
| ![\begin{displaymath}
=\ \ \ -\ {\Delta z \over \ 4} \
[( q_{n+1} \ +\ q_n )^ { {\rm *} \, }
( R\ +\ R^ { {\rm *} \, } )\,( q_{n+1} \ +\ q_n )]\end{displaymath}](img225.gif) |
(86) |
This equation establishes the result:
If the matrix 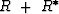 is
positive definite,
then
is
positive definite,
then 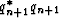 is less than
is less than 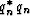 .
.





Next: Application to 45 degree
Up: THE BULLETPROOFING OF MUIR
Previous: Stability of the differential
Stanford Exploration Project
10/31/1997
![]()
![]()