




Next: Gazdag's v(x) method
Up: TUNING UP FOURIER MIGRATIONS
Previous: Controlling Stolt migration wraparound
The great strength and the great weakness of the Stolt migration method
is that it uses Fourier transformation over depth.
This is a strength because it makes his method much faster
than all other methods.
And it is a weakness because it requires a velocity that is
a constant function of depth.
The earth velocity typically ranges over a factor of two
within the seismic section, and the effect of velocity on migration
tends to go as its square.
To ameliorate this difficulty, Stolt suggested stretching the time axis
to make the data look more like it had come from a constant-velocity earth.
Stolt proposed the stretching function
| 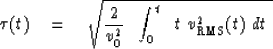 |
(6) |
where
| 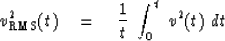 |
(7) |
At late times, which are associated with high velocities,
Stolt's stretch implies that  grows faster than t.
The
grows faster than t.
The  -axis is uniformly sampled to allow
the fast Fourier transform.
Thus at late time the samples are increasingly dense on the t-axis.
This is the opposite of what earth Q and the sampling theorem suggest,
but most people consider this a fair price.
-axis is uniformly sampled to allow
the fast Fourier transform.
Thus at late time the samples are increasingly dense on the t-axis.
This is the opposite of what earth Q and the sampling theorem suggest,
but most people consider this a fair price.
The most straightforward derivation of (6) and (7) is
based on the idea of matching the
curvature of ideal hyperbola tops to the curvature on the stretched data.
The equation of an ideal hyperbola in  -space is
-space is
|  |
(8) |
Simple differentiation shows that the curvature at the hyperbola top is
| 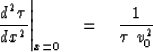 |
(9) |
It can be shown that in a stratified medium,
equation (9) applies,
except that the velocity must be replaced by the RMS velocity:
| 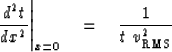 |
(10) |
We seek a stretched time 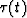 .We would like to match the curves t (x) and
.We would like to match the curves t (x) and 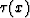 for all x.
But that would overdetermine the problem.
Instead we could just match the derivatives at the hyperbola top,
i.e.,
the second derivative of
for all x.
But that would overdetermine the problem.
Instead we could just match the derivatives at the hyperbola top,
i.e.,
the second derivative of ![$\tau [t(x)]$](img71.gif) with respect to x at x=0.
With the substitutions (9) and (10),
this would give an expression for
with respect to x at x=0.
With the substitutions (9) and (10),
this would give an expression for 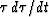 which, after integrating
and taking its square root, yields (6) and (7).
which, after integrating
and taking its square root, yields (6) and (7).
A different derivation of the stretch gives
a more accurate result at steeper angles.
Instead of matching hyperbola curvature at the top,
we go some distance out on the flank and
match the slope and value.
It is the flanks of the hyperbola that actually migrate,
not the tops, so this result is more accurate.
Algebraically the derivation is also easier, because only
first
derivatives are needed.
Differentiating equation (8) with respect to x for
a reflector at any depth zj gives
| 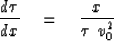 |
(11) |
There is an analogous expression in a stratified medium.
To obtain it,
solve 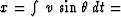
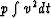 for p = dt/dx:
for p = dt/dx:
| 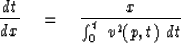 |
(12) |
Expressions (11) and (12)
play the same role as (9) and (10),
but (11) and (12) are valid everywhere,
not just at the hyperbola top.
Differentiating 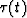 gives
gives
| 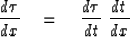 |
(13) |
Inserting (11) and (12) into (13) gives
| 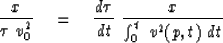 |
(14) |
| ![\begin{displaymath}
\tau \ d \tau \eq \left[ \
{1 \over v_0^2} \
\int_0^t \ v^2 (p,t ' ) \ dt '
\ \right] \ dt\end{displaymath}](img79.gif) |
(15) |
Integrating (15) gives 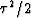 on the left.
Then,
taking the square root gives (6) but with a new definition for
RMS velocity:
on the left.
Then,
taking the square root gives (6) but with a new definition for
RMS velocity:
| 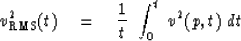 |
(16) |
The thing that is new is the presence of the Snell parameter p.
In a stratified medium characterized by some velocity,
say, v ' (z),
the velocity v(p,t) is defined for the tip of the ray
that left the surface at an angle with a stepout p.
In practice, what value of p should be used?
The best procedure is to look at the data and measure the 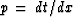 of
those events that you wish to migrate well.
A default value is
of
those events that you wish to migrate well.
A default value is
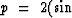 30
30 )/(2.5 km/sec) = .4 millisec/meter.
The factor of 2 is from the exploding-reflector model.
)/(2.5 km/sec) = .4 millisec/meter.
The factor of 2 is from the exploding-reflector model.





Next: Gazdag's v(x) method
Up: TUNING UP FOURIER MIGRATIONS
Previous: Controlling Stolt migration wraparound
Stanford Exploration Project
10/31/1997
![]() -space is
-space is
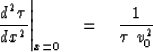
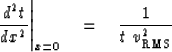
![]() of
those events that you wish to migrate well.
A default value is
of
those events that you wish to migrate well.
A default value is
![]() 30
30![]() )/(2.5 km/sec) = .4 millisec/meter.
The factor of 2 is from the exploding-reflector model.
)/(2.5 km/sec) = .4 millisec/meter.
The factor of 2 is from the exploding-reflector model.