




Next: ADAPTIVE FILTERS
Up: Waveform applications of least
Previous: PREDICTION AND SHAPING FILTERS
The uncertainty principle says
that if a time function contains most of its energy
in the time-span 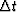 ,
then its Fourier transform contains most of its energy
in a bandwidth
,
then its Fourier transform contains most of its energy
in a bandwidth 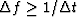 .
This is not the same as saying
that if we have a sample of a stationary time series
of length
.
This is not the same as saying
that if we have a sample of a stationary time series
of length 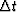 ,the best frequency resolution we can hope to attain will be
,the best frequency resolution we can hope to attain will be
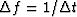 .The difference lies in the difference between assuming a
function is zero outside the interval
.The difference lies in the difference between assuming a
function is zero outside the interval 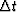 in which it is
given and in assuming that it continues ``in a sensible way"
outside the given interval.
If the data sample can be continued ``in a sensible way"
some distance beyond the interval in which it is given,
then the frequency resolution
in which it is
given and in assuming that it continues ``in a sensible way"
outside the given interval.
If the data sample can be continued ``in a sensible way"
some distance beyond the interval in which it is given,
then the frequency resolution 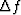 may be considerably
smaller than
may be considerably
smaller than 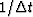 .A finer resolution depends upon the predictability of the data
off the ends of the sample. If one has a segment of
a stationary series which is short compared to the
autocorrelation of the stationary series,
then the spectral estimation procedure of John P. Burg
will be radically better than any truncated Fourier
transform method. This comes about in physical
problems when one is dealing with resonances which
have decay times that are long compared to the
observation time or when one is looking at a function of
space where each point in space represents another
instrument.
.A finer resolution depends upon the predictability of the data
off the ends of the sample. If one has a segment of
a stationary series which is short compared to the
autocorrelation of the stationary series,
then the spectral estimation procedure of John P. Burg
will be radically better than any truncated Fourier
transform method. This comes about in physical
problems when one is dealing with resonances which
have decay times that are long compared to the
observation time or when one is looking at a function of
space where each point in space represents another
instrument.
If a spectrum R(Z) is estimated by
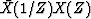 where X(Z) is a
polynomial made up from N + 1 known data points,
then the coefficients of R(Z) are computed by
where X(Z) is a
polynomial made up from N + 1 known data points,
then the coefficients of R(Z) are computed by
| 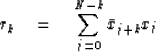 |
(8) |
Notice that r0 is calculated from N + 1 terms,
r1 from N terms, etc. If N is not large enough,
this will have an undesirable biasing effect.
The biasing is removed if the rk are computed
instead by the formula
| 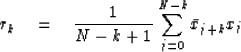 |
(9) |
The trouble with using (9) is that data samples
can easily be found for which rk will not be a valid
autocorrelation function. For example,
the spectrum will not be positive at all frequencies,
the solution to Toeplitz equations may blow up, etc.
Burg's approach avoids the end-effect problems of
(8) and the possibility of impossible results
from (9). Instead of estimating the
autocorrelation rk directly from the data he estimates
a minimum-phase prediction-error filter directly from the data.
The output of a prediction-error filter
has a white spectrum. (If it did not,
then the color could be used to improve prediction.)
Since the spectrum of the output is the spectrum of the input
times the spectrum of the filter,
the spectrum of the input may be estimated as the inverse
of the spectrum of the prediction-error filter.
As we have seen, narrow spectral peaks are far more
easily represented by a denominator than by a numerator.
Let the given segment of data be denoted by
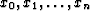 .Then a two-term prediction-error filter
(1,a) of the time series xt is given
by the choice of a which minimizes
.Then a two-term prediction-error filter
(1,a) of the time series xt is given
by the choice of a which minimizes
| 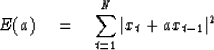 |
(10) |
Unfortunately,
consideration of a few examples shows that
there exist time series [like (1,2)] for which
|a| may turn out to be greater than unity.
This is unacceptable because the prediction-error
filter is not minimum-phase,
the spectrum is not positive, etc.
Recall that a prediction-error filter defined in the
previous section depends only on the autocorrelation of the
data and not the data per se.
This means that the same filter is
computed from both a time series and
from the (complex-conjugate) time-reversed time series.
This suggests that the error of forward prediction
(10) be augmented by the error of backward
prediction. That is
| 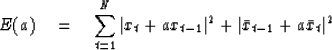 |
(11) |
We will later establish that the minimization of
(11) always leads to an |a| less than unity.
The power spectral estimate associated with this
value of a is
![$R = 1/[(1 + \bar{a}/Z)(1 + aZ)]$](img31.gif) .The value of
.The value of 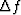 may be very small if
a turns out very close to the unit circle.
may be very small if
a turns out very close to the unit circle.
A natural extension of (11) to filters
with more terms would seem to be to minimize
| 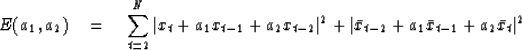 |
(12) |
Unfortunately,
Burg discovered time series for which the computed filter
A(Z) = 1 + a1 Z + a2 Z2 was not minimum-phase.
If A(Z) is not minimum-phase,
then ![$R = 1/[\bar{A}(1/Z)A(Z)]$](img33.gif) is not a satisfactory
spectral estimate because R(Z) is to be evaluated
on the unit circle and 1/A(Z) would not be convergent there.
is not a satisfactory
spectral estimate because R(Z) is to be evaluated
on the unit circle and 1/A(Z) would not be convergent there.
Burg noted that the Levinson recursion always gives
minimum-phase filters.
In the Levinson recursion a filter of order 3 is built up
from one of order 2 by
Thus Burg decided that instead of using least squares
to determine a1 and a2 as in (12),
he would take a to be given from (11)
and then do a least-squares problem to solve for c.
This would be done in such a way as to ensure that
|c| comes out less than unity,
which guarantees that A(Z) = 1 + a1 Z + a2 Z2 is
minimum-phase. Thus he suggested rewriting (12) as
| 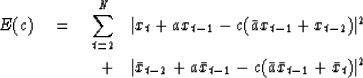 |
|
| (13) |
Now the error (13),
which is the sum of the error of forward prediction plus
the error of backward prediction,
is minimized with respect to variation of c.
(In a later chapter we will see fit to call c
a reflection coefficient.)
The quantity a remains fixed by the minimization of (11).
Now let us establish that |c| is less than unity.
Denote by e+ the time series
xt + axt-1 which is the error in forward prediction
of xt. Denote by e- the time series
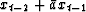 of error on backward prediction.
With this, (13) becomes
of error on backward prediction.
With this, (13) becomes
| 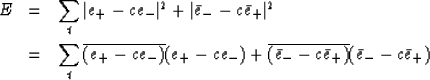 |
|
| (14) |
Setting the derivative with respect to 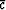 equal to zero
equal to zero
| 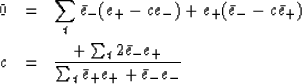 |
|
| (15) |
(One may note that 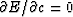 gives the
same result.) That |c| is always less than unity may
be seen by noting that the length of the vector
gives the
same result.) That |c| is always less than unity may
be seen by noting that the length of the vector
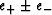 is always positive. In particular
is always positive. In particular
| 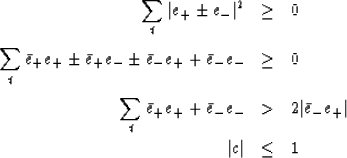 |
|
| |
| |
| (16) |
If we now redefine e+ and e- as
| 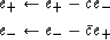 |
(17) |
| (18) |
we have the forward and backward prediction errors of the
three-term filter 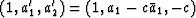 .One can then return to (14)
and proceed recursively.
As the recursion proceeds e+ and e- gradually
become unpredictable random numbers.
We have then found a filter A(Z) which filters
X(Z) either forward or backward and the output must
be the inverse of the spectrum of the filter.
.One can then return to (14)
and proceed recursively.
As the recursion proceeds e+ and e- gradually
become unpredictable random numbers.
We have then found a filter A(Z) which filters
X(Z) either forward or backward and the output must
be the inverse of the spectrum of the filter.
In later chapters we will discover a wave-propagation
interpretation of the Burg algorithm.
In a layered medium the parameters ck have the
interpretation of the up- and downgoing waves;
and the whole process of calculating a succession of
ck amounts to downward continuing surface
seismograms into the earth, determining an earth model
ck as you go.
EXERCISES:
- Consider the time series with ten points
(1, 1, 1, -1, -1, -1, 1, 1, 1, -1).
Compute C and A up to cubics in Z.
Compare the autocorrelation rt calculated by
Burg's method with R(Z) estimated from the
truncated sample and with R(Z) estimated by intuitively
extending the data sample in time to plus and minus infinity.
- Modify the program of Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to compute
and include the scale factor V which belongs in the
spectrum.
to compute
and include the scale factor V which belongs in the
spectrum.





Next: ADAPTIVE FILTERS
Up: Waveform applications of least
Previous: PREDICTION AND SHAPING FILTERS
Stanford Exploration Project
10/30/1997
![]() where X(Z) is a
polynomial made up from N + 1 known data points,
then the coefficients of R(Z) are computed by
where X(Z) is a
polynomial made up from N + 1 known data points,
then the coefficients of R(Z) are computed by
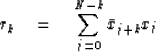
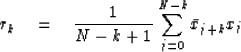
![]() .Then a two-term prediction-error filter
(1,a) of the time series xt is given
by the choice of a which minimizes
.Then a two-term prediction-error filter
(1,a) of the time series xt is given
by the choice of a which minimizes
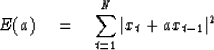
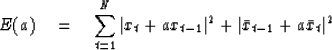
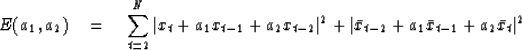
![\begin{eqnarraystar}
\left[
\begin{array}
{l}
1 \\ a_1 \\ a_2 \end{array} \ri...
...c \left[
\begin{array}
{c}
0 \\ a \\ 1 \end{array} \right] \end{eqnarraystar}](img34.gif)
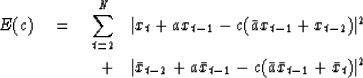
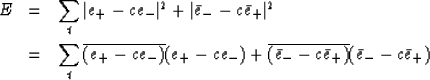
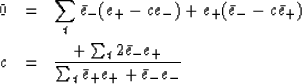
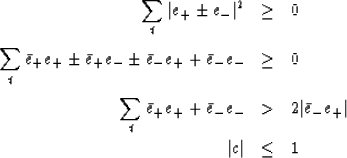
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to compute
and include the scale factor V which belongs in the
spectrum.
to compute
and include the scale factor V which belongs in the
spectrum.