




Next: WEIGHTS AND CONSTRAINTS
Up: Data modeling by least
Previous: Data modeling by least
When there are more linear equations than unknowns,
it is usually impossible
to find a solution which satisfies all the equations.
Then one often looks for a solution
which approximately satisfies all the equations.
Let a and c be known
and x be unknown in the following set of equations
where there are more equations than unknowns.
| ![\begin{displaymath}
\left[
\begin{array}
{cccc}
a_{11} & a_{12} & \cdots & a_{...
...{c}
c_1 \\
c_2 \\
\vdots \\ c_n \\ \end{array} \right]\end{displaymath}](img11.gif) |
(1) |
Usually there will be no set of
xi which exactly satisfies (1).
Let us define an error vector ej by
| ![\begin{displaymath}
\left[
\begin{array}
{cccc}
a_{11} & a_{12} & \cdots & a_{...
...
{c}
e_1 \\
e_2 \\
\vdots \\ e_n \\ \end{array} \right]\end{displaymath}](img12.gif) |
(2) |
It simplifies the development to rewrite this equation as follows
(a trick I learned from John P. Berg).
| ![\begin{displaymath}
\left[
\begin{array}
{cccc}
-c_1 & a_{11} & \cdots & a_{1m...
...
{c}
e_1 \\
e_2 \\
\vdots \\ e_n \\ \end{array} \right]\end{displaymath}](img13.gif) |
(3) |
We may abbreviate this equation as
| 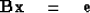 |
(4) |
where B is the matrix containing c and a.
The ith error may be written
as a dot product and either vector may be written as the column
Now we will minimize the sum squared error
E defined as 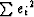
| ![\begin{displaymath}
E \eq \sum_i [1 \quad x_1 \quad \cdots]
\; \left[
\begin{a...
...\begin{array}
{c}
1 \\
x_1 \\
\vdots \end{array} \right]\end{displaymath}](img17.gif) |
(5) |
The summation may be brought inside the constants
| ![\begin{displaymath}
E \eq [1 \quad x_1 \quad x_2 \quad \cdots]
\; \left\{
\sum...
...ay}
{c}
1 \\
x_1 \\
x_2 \\
\vdots \end{array} \right]\end{displaymath}](img18.gif) |
(6) |
The matrix in the center,
call it rij,
is symmetrical.
It is a positive (more strictly, nonnegative)
definite matrix because you will never be able
to find an x for which E is negative,
since E is a sum of squared ei.
We find the x with minimum E by requiring
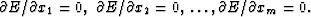 Notice that this will give us exactly one
equation for each unknown.
In order to clarify the presentation we will
specialize (6) to two unknowns.
Notice that this will give us exactly one
equation for each unknown.
In order to clarify the presentation we will
specialize (6) to two unknowns.
| ![\begin{displaymath}
E
\eq [1 \quad x_1 \quad x_2]
\; \left[
\begin{array}
{ccc...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img20.gif) |
(7) |
Setting to zero the derivative with respect to x1, we get
| ![\begin{displaymath}
0 \eq {\partial E \over \partial x_1}
\eq [0 \quad 1 \quad ...
...left[
\begin{array}
{c}
0 \\
1 \\
0 \end{array} \right]\end{displaymath}](img21.gif) |
(8) |
Since rij = rji,
both terms on the right are equal.
Thus (8) may be written
| ![\begin{displaymath}
0 \eq {\partial E \over \partial x_1}
\eq 2 [r_{10} \quad r...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img22.gif) |
(9) |
Likewise,
differentiating with respect to x2 gives
| ![\begin{displaymath}
0 \eq {\partial E \over \partial x_2}
\eq 2 [r_{20} \quad r...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img23.gif) |
(10) |
Equations (9) and (10) may be combined
| ![\begin{displaymath}
\left[
\begin{array}
{c}
0 \\
0 \end{array} \right]
\e...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img24.gif) |
(11) |
This form is two equations in two unknowns.
One might write it in the more conventional form
| ![\begin{displaymath}
\left[
\begin{array}
{cc}
r_{11} & r_{12} \\ r_{21} & r_{...
...ft[
\begin{array}
{c}
r_{10} \\
r_{20} \end{array} \right]\end{displaymath}](img25.gif) |
(12) |
The matrix of (11) lacks
only a top row to be equal to the matrix
of (7).
To give it that row,
we may augment (11) by
| 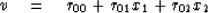 |
(13) |
where (13) may be regarded
as a definition of a new variable v.
Putting (13) on top of (11) we get
| ![\begin{displaymath}
\left[
\begin{array}
{c}
v \\
0 \\
0 \end{array} \ri...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img27.gif) |
(14) |
The solution x of (12)
or (14) is that set of
xk for which E is a minimum.
To get an interpretation of v, we may
multiply both sides by ![$[1 \quad x_1 \quad x_2]$](img28.gif) ,
getting
,
getting
| ![\begin{displaymath}
v \eq [1 \quad x_1 \quad x_2]
\; \left[
\begin{array}
{c}
...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img29.gif) |
(15) |
Comparing (15) with (7),
we see that v is the minimum value of E.
Occasionally,
it is more convenient to have the essential equations in
partitioned matrix form.
In partitioned matrix form,
we have for the error (6)
| ![\begin{displaymath}
E \eq [1 \ \vdots \ {\bf x}]^T
\left[
\begin{array}
{c}
-...
...1 \\ \hbox to 0.25in{\dotfill} \\ {\bf x} \end{array} \right]\end{displaymath}](img30.gif) |
(16) |
The final equation (14) splits into
| 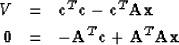 |
(17) |
| (18) |
where (18) represents
simultaneous equations to be solved for x.
Equation (18) is what you have to set up in a computer.
It is easily remembered by a quick and dirty
(very dirty) derivation.
That is,
we began with the overdetermined equations
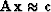 ;premultiplying by
;premultiplying by 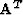 gives
gives 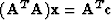 which is (18).
which is (18).
In physical science applications,
the variable zj is frequently a complex
variable, say zj = xj + iyj.
It is always possible to go through the
foregoing analyses,
treating the problem as though xi and yi were
real independent variables.
There is a considerable gain in simplicity and a
saving in computational effort
by treating zj as a single complex variable.
The error E may be regarded
as a function of either xj and yj or
zj and 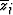 .
In general
.
In general 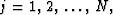 but we will
treat the case N = 1 here
and leave the general case for the Exercises.
The minimum is found where
but we will
treat the case N = 1 here
and leave the general case for the Exercises.
The minimum is found where
| 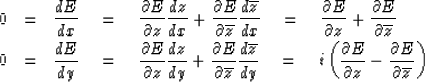 |
(19) |
| (20) |
Multiplying (20) by i
and adding and subtracting these equations,
we may express the minimum condition more simply as
| 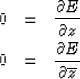 |
(21) |
| (22) |
However,
the usual case is that E is a positive real quadratic function of
z and 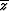 and that
and that
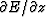 is merely the complex
conjugate of
is merely the complex
conjugate of 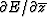 .
Then the two conditions
(21) and (22)
may be replaced by either one of them.
Usually,
when working with complex variables we are minimizing a positive
quadratic form like
.
Then the two conditions
(21) and (22)
may be replaced by either one of them.
Usually,
when working with complex variables we are minimizing a positive
quadratic form like
| 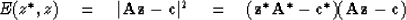 |
(23) |
where * denotes complex-conjugate transpose.
Now (22) gives
| 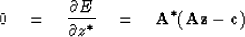 |
(24) |
which is just the complex form of (18).
Let us consider an example.
Suppose a set of wave arrival times ti is
measured at sensors located on the x axis at points xi.
Suppose the wavefront is to be fitted to a
parabola 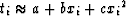 .Here,
the xi are knowns and a, b, and c are unknowns.
For each sensor i we have an equation
.Here,
the xi are knowns and a, b, and c are unknowns.
For each sensor i we have an equation
| ![\begin{displaymath}[-t_i\quad 1 \quad x_i \quad {x_i}^2]
\; \left[
\begin{array}...
...\
a \\
b \\
c \end{array} \right]
\quad\approx\quad 0\end{displaymath}](img45.gif) |
(25) |
When i has greater range than 3
we have more equations than unknowns.
In this example, (14) takes the form
| ![\begin{displaymath}
\left\{ \sum^n_{i = 1}
\left[ \begin{array}
{c}
-t_i \\ ...
...begin{array}
{c}
v \\
0 \\
0 \\
0 \end{array} \right]\end{displaymath}](img46.gif) |
(26) |
This may be solved by standard methods for a, b, and c.
The last three rows of (26) may be written
| ![\begin{displaymath}
\sum^n_{i = 1}
\left[ \begin{array}
{c}
1 \\
x_i \\
...
...left[
\begin{array}
{c}
0 \\
0 \\
0 \end{array} \right]\end{displaymath}](img47.gif) |
(27) |
This says the error vector ei is
perpendicular (or normal) to the functions
1, x, and x2,
which we are fitting to the data.
For that reason these
equations are often called normal equations.
EXERCISES:
- Extend (24) by fitting waves observed in the x,
y plane to a two-dimensional quadratic.
- Let y(t) constitute a complex-valued function
at successive integer values of t.
Fit y(t) to a least-squares straight line
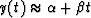 where
where
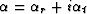 and
and 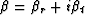 .
Do it two ways: (a) Assume
.
Do it two ways: (a) Assume 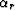 ,
, 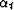 ,
,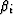 , and
, and 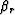 are four independent variables,
and (b) Assume
are four independent variables,
and (b) Assume
 ,
, 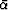 ,
, 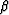 , and
, and 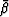 are independent
variables. (Leave answer in terms of
are independent
variables. (Leave answer in terms of 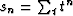 .)
.)
- Equation (14) has assumed all quantities are real.
Generalize equation (14) to all complex quantities.
Verify that the matrix is Hermitian.
- At the jth seismic observatory (latitude xj, longitude yj)
earthquake waves are observed to arrive at time tj.
It has been conjectured
that the earthquake has an origin time t,
latitude x, and longitude y.
The theoretical travel time may be looked up
in a travel time table
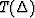 where T is the travel time and
where T is the travel time and
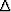 is the great circle angle.
One has
is the great circle angle.
One has
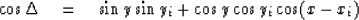
The time residual at the jth station,
supposing that the earthquake
occurred at (x, y, t), is
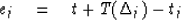
The time residual,
supposing that the earthquake occurred at
(x + dx, y + dy, t + dt), is
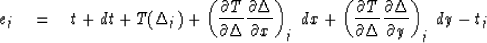
Find equations to solve for dx,
dy, and dt which minimize the
sum-squared time residuals.
- Gravity gj has been measured at
N irregularly spaced points on the
surface of the earth
(colatitude xj, longitude yj, j = 1, N).
Show that the matrix of the normal equation
which fits the data to spherical
harmonics may be written as a sum of a column times its transpose,
as in the preceding problem.
How would the matrix simplify if there were infinitely
many uniformly spaced data points?
(NOTE: Spherical harmonics S are the class of functions
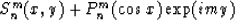
for 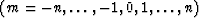 and
and
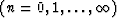 where Pmn is an associated Legendre polynomial of degree n
and order m.)
where Pmn is an associated Legendre polynomial of degree n
and order m.)
- Ocean tides fit sinusoidal functions of
known frequencies quite accurately.
Associated with the tide is an earth tilt.
A complex time series
may be made from the north-south tilt plus
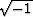 times the east-west tilt.
The observed complex time series may be fitted to an analytical form
times the east-west tilt.
The observed complex time series may be fitted to an analytical form
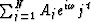 .
Find a set of equations which may be
solved for the Aj which gives the best fit
of the formula to the data.
Show that some elements of the normal equation matrix
are sums which may
be summed analytically.
.
Find a set of equations which may be
solved for the Aj which gives the best fit
of the formula to the data.
Show that some elements of the normal equation matrix
are sums which may
be summed analytically.
- The general solution to Laplace's equation
in cylindrical coordinates
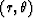 for a potential field P
which vanishes at
for a potential field P
which vanishes at 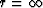 is given by
is given by
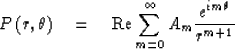
Find the potential field surrounding
a square object at the origin which is
at unit potential.
Do this by finding N of the coefficients
Am by minimizing the squared difference
between 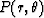 and unity integrated
around the square.
Give the answer in terms of an inverse matrix of integrals.
Which coefficients Am vanish exactly by symmetry?
and unity integrated
around the square.
Give the answer in terms of an inverse matrix of integrals.
Which coefficients Am vanish exactly by symmetry?





Next: WEIGHTS AND CONSTRAINTS
Up: Data modeling by least
Previous: Data modeling by least
Stanford Exploration Project
10/30/1997
![\begin{displaymath}
\left[
\begin{array}
{cccc}
a_{11} & a_{12} & \cdots & a_{...
...{c}
c_1 \\
c_2 \\
\vdots \\ c_n \\ \end{array} \right]\end{displaymath}](img11.gif)
![\begin{displaymath}
\left[
\begin{array}
{cccc}
a_{11} & a_{12} & \cdots & a_{...
...{c}
c_1 \\
c_2 \\
\vdots \\ c_n \\ \end{array} \right]\end{displaymath}](img11.gif)
![\begin{displaymath}
\left[
\begin{array}
{cccc}
a_{11} & a_{12} & \cdots & a_{...
...
{c}
e_1 \\
e_2 \\
\vdots \\ e_n \\ \end{array} \right]\end{displaymath}](img12.gif)
![\begin{displaymath}
\left[
\begin{array}
{cccc}
-c_1 & a_{11} & \cdots & a_{1m...
...
{c}
e_1 \\
e_2 \\
\vdots \\ e_n \\ \end{array} \right]\end{displaymath}](img13.gif)
![\begin{eqnarraystar}
e_i
\eq [b_{i1} \quad b_{i2}\quad \cdots]
\;
\left[
\beg...
...1} \\
b_{i2} \\
\vdots \end{array} \right] \nonumber \\ \end{eqnarraystar}](img15.gif)
![\begin{displaymath}
E \eq \sum_i [1 \quad x_1 \quad \cdots]
\; \left[
\begin{a...
...\begin{array}
{c}
1 \\
x_1 \\
\vdots \end{array} \right]\end{displaymath}](img17.gif)
![\begin{displaymath}
E \eq [1 \quad x_1 \quad x_2 \quad \cdots]
\; \left\{
\sum...
...ay}
{c}
1 \\
x_1 \\
x_2 \\
\vdots \end{array} \right]\end{displaymath}](img18.gif)
![\begin{displaymath}
E
\eq [1 \quad x_1 \quad x_2]
\; \left[
\begin{array}
{ccc...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img20.gif)
![\begin{displaymath}
0 \eq {\partial E \over \partial x_1}
\eq [0 \quad 1 \quad ...
...left[
\begin{array}
{c}
0 \\
1 \\
0 \end{array} \right]\end{displaymath}](img21.gif)
![\begin{displaymath}
0 \eq {\partial E \over \partial x_1}
\eq 2 [r_{10} \quad r...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img22.gif)
![\begin{displaymath}
0 \eq {\partial E \over \partial x_2}
\eq 2 [r_{20} \quad r...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img23.gif)
![\begin{displaymath}
\left[
\begin{array}
{c}
0 \\
0 \end{array} \right]
\e...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img24.gif)
![\begin{displaymath}
\left[
\begin{array}
{c}
v \\
0 \\
0 \end{array} \ri...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img27.gif)
![\begin{displaymath}
v \eq [1 \quad x_1 \quad x_2]
\; \left[
\begin{array}
{c}
...
...[
\begin{array}
{c}
1 \\
x_1 \\
x_2 \end{array} \right]\end{displaymath}](img29.gif)
![\begin{displaymath}
E \eq [1 \ \vdots \ {\bf x}]^T
\left[
\begin{array}
{c}
-...
...1 \\ \hbox to 0.25in{\dotfill} \\ {\bf x} \end{array} \right]\end{displaymath}](img30.gif)
![]() .
In general
.
In general ![]() but we will
treat the case N = 1 here
and leave the general case for the Exercises.
The minimum is found where
but we will
treat the case N = 1 here
and leave the general case for the Exercises.
The minimum is found where
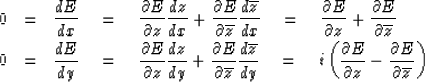
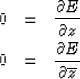
![]() and that
and that
![]() is merely the complex
conjugate of
is merely the complex
conjugate of ![]() .
Then the two conditions
(21) and (22)
may be replaced by either one of them.
Usually,
when working with complex variables we are minimizing a positive
quadratic form like
.
Then the two conditions
(21) and (22)
may be replaced by either one of them.
Usually,
when working with complex variables we are minimizing a positive
quadratic form like
![]() .Here,
the xi are knowns and a, b, and c are unknowns.
For each sensor i we have an equation
.Here,
the xi are knowns and a, b, and c are unknowns.
For each sensor i we have an equation
![\begin{displaymath}[-t_i\quad 1 \quad x_i \quad {x_i}^2]
\; \left[
\begin{array}...
...\
a \\
b \\
c \end{array} \right]
\quad\approx\quad 0\end{displaymath}](img45.gif)
![\begin{displaymath}
\left\{ \sum^n_{i = 1}
\left[ \begin{array}
{c}
-t_i \\ ...
...begin{array}
{c}
v \\
0 \\
0 \\
0 \end{array} \right]\end{displaymath}](img46.gif)
![\begin{displaymath}
\sum^n_{i = 1}
\left[ \begin{array}
{c}
1 \\
x_i \\
...
...left[
\begin{array}
{c}
0 \\
0 \\
0 \end{array} \right]\end{displaymath}](img47.gif)
![]()
![]()
![]()
![]()
![]()