Violations of causality often result from seemingly inconsequential approximations at spectral frequencies outside the range of practical interest. The seemingly inconsequential approximations often take on significance because of the very weak convergence in the Hilbert transform. With regard to (1) and (2), the violation of causality may turn out to be a low price to pay compared with the cost of a more precise analysis. With regard to (3) or computation in general, the violation of causality usually has disastrous consequences. Even though difference equations may have proper behavior at frequencies of interest, exponential growth at other frequencies is almost always so severe as to completely obliterate the desired solution.
Most wave-propagation theories are worked out in the frequency domain in homogeneous materials. If they are further done in cartesian geometry, the end result is that propagation along the x axis is given by
| |
(23) |
|
3-7
Figure 7 Modeling wave propagation with filters. | 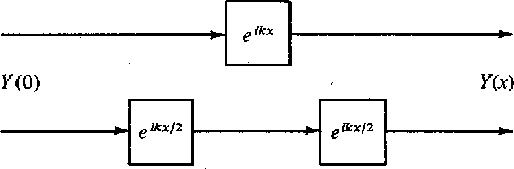 |
First, consider the simple case when ![]() is real for all real
is real for all real ![]() .Then eikx is an all-pass filter.
It is realizable
if and only if
.Then eikx is an all-pass filter.
It is realizable
if and only if ![]() is a monotonically increasing function
of
is a monotonically increasing function
of ![]() .
.
Next, suppose ![]() is complex.
This means that attenuation will occur.
Clearly energy conservation requires that the real part of ikx be negative.
is complex.
This means that attenuation will occur.
Clearly energy conservation requires that the real part of ikx be negative.
Define P(Z) to be a realizable all-pass filter and B(Z) to be a realizable minimum-phase wavelet. Any realizable function can be represented in the form B(Z) P(Z). We will require eikx to be so represented.
| |
(24) |
| |
(25) |
First of all, from the attenuation ![]() we can by Hilbert
transform compute
we can by Hilbert
transform compute ![]() .When it is subtracted from kr x we are
left with the phase shift
.When it is subtracted from kr x we are
left with the phase shift ![]() of the all-pass filter.
Recall from Sec. 2-6 (on all-pass filters) that
if and only if
of the all-pass filter.
Recall from Sec. 2-6 (on all-pass filters) that
if and only if ![]() is monotonically increasing,
we have a causal all-pass filter.
In conclusion, the test of causality for a function
is monotonically increasing,
we have a causal all-pass filter.
In conclusion, the test of causality for a function ![]() lies in computing
lies in computing ![]() and seeing whether it is monotonically increasing for all frequencies.
and seeing whether it is monotonically increasing for all frequencies.
A great deal of confusion results from attenuation laws which are thought
to be of the form ![]() (gaussian attenuation)
or
(gaussian attenuation)
or ![]() (sometimes called constant Q).
The reason is that these functions are not integrable
so they do not have convergent Hilbert transforms;
that is,
the
(sometimes called constant Q).
The reason is that these functions are not integrable
so they do not have convergent Hilbert transforms;
that is,
the ![]() turns out to be infinite.
These functions correspond to time pulses
like the gaussian time function e-t2 which
do not have a time before which they are zero.
Such functions cannot strictly be considered
to be associated with any causal process;
however, they may give excellent practical approximations.
In reality, physical dissipation is generally associated
with a relaxation phenomenon having a finite relaxation time.
For frequency values below the relaxation value, the
attenuation may appear to be increasing indefinitely with frequency,
but, in fact, the attenuation decreases
above the characteristic relaxation frequency.
The attenuation also provides a phase velocity aberration
because of the addition of
turns out to be infinite.
These functions correspond to time pulses
like the gaussian time function e-t2 which
do not have a time before which they are zero.
Such functions cannot strictly be considered
to be associated with any causal process;
however, they may give excellent practical approximations.
In reality, physical dissipation is generally associated
with a relaxation phenomenon having a finite relaxation time.
For frequency values below the relaxation value, the
attenuation may appear to be increasing indefinitely with frequency,
but, in fact, the attenuation decreases
above the characteristic relaxation frequency.
The attenuation also provides a phase velocity aberration
because of the addition of ![]() to
to ![]() but this is generally considered to be too small to measure.
but this is generally considered to be too small to measure.
Now let us take up an example of computer modeling of wave propagation.
The simplest example is propagation without dissipation.
Then ![]() where v is the velocity.
Rather than attempt to construct a filter which
will carry waves a long distance
we will only attempt to carry them a distance
where v is the velocity.
Rather than attempt to construct a filter which
will carry waves a long distance
we will only attempt to carry them a distance ![]() .The filter may be used N times to propagate a distance
.The filter may be used N times to propagate a distance
![]() .We will use the bilinear truncation of the power series for exponential
.We will use the bilinear truncation of the power series for exponential
| |
(26) |
| |
(27) |
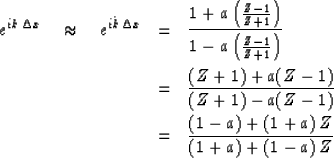 |
||
| (28) |
| |
(29) |
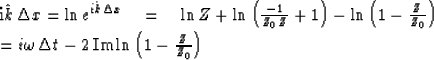 |
||