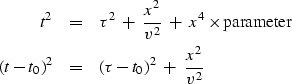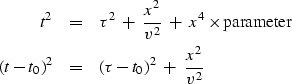Next: Can I abandon the
Up: CURVED WAVEFRONTS
Previous: Layered media
Occasionally data does not fit a hyperbolic curve very well.
Two other simple fitting functions are
| 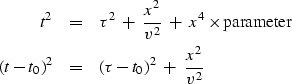 |
(34) |
| (35) |
Equation (34) has an extra adjustable parameter
of no simple interpretation other than the beginning of a power series in x2.
I prefer Equation (35) where the extra adjustable parameter
is a time shift t0 which has a simple interpretation,
namely, a time shift
such as would result from a near-surface low velocity layer.
In other words, a datum correction.
1





Next: Can I abandon the
Up: CURVED WAVEFRONTS
Previous: Layered media
Stanford Exploration Project
12/26/2000