 |
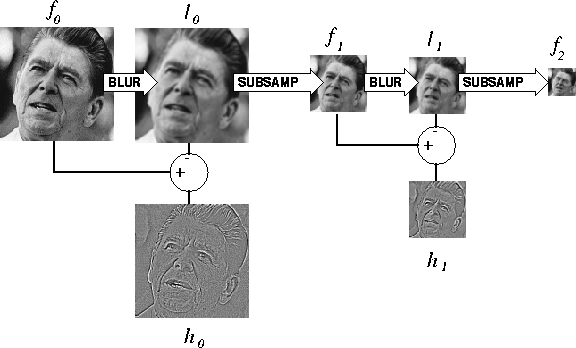
Figure 1 Decomposition step for two-level Laplacian Pyramid. The finished pyramid consists of the two ``highpass'' bands, h0 and h1, and the ``lowpass'' band, f2.
The general class of linear transform decomposes an image into various components by multiplication with a set of transform functions. Some examples are the Discrete Fourier and Discrete Cosine Transforms, the Singular Value Decomposition, and finally, the Wavelet Transform, of which the Laplacian Pyramid and other subband transforms are simple ancestors.
Real-world digital images are in general both scale-variant and highly nonstationary in space. They contain a variety of objects and features (lines, shapes, patterns, edges) at differerent scales, orientations, and spatial locations; features which the ideal image transformation should independently extract into easily manipulable components ().
The Laplacian Pyramid decomposition, originally developed by Burt and Adelson , is illustrated in Figure 1 for a two-level pyramid. The following pseudocode describes the simple process for a pyramid with an arbitrary number of levels.
|
Notice from the pseudocode that the pyramid consists of nScales ``highpass'' bands hi and a ``lowpass'' band, .The hi contain most of the image's important textural features, at different scales. The Laplacian Pyramid is named as such because the process of computing hi by subracting a blurred copy fi from fi is equivalent to convolving fi with (approximately) the Laplacian of the Gaussian blurring filter.
 |
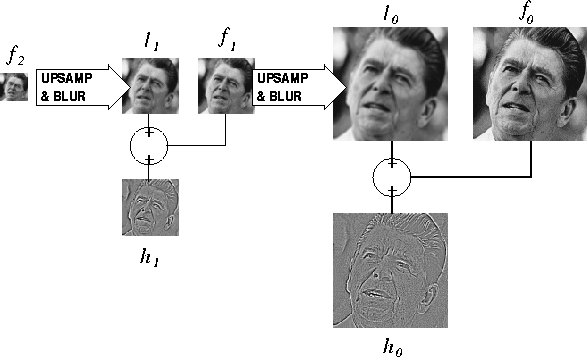
The reconstruction step for a two-level Laplacian Pyramid proceeds in preditictable faction, and is illustrated in figure 2. The following pseudocode describes the process for a pyramid with an arbitrary number of scales.
|
The function upSamp2() simply inserts zeros between the samples of fi, raising its size by a factor of two.
 |